Goals and Review for Learning Measurement on
Waves & Acoustics
This Learning Measurement will cover everything we've done so far this semester. Reread the notes pages, and review the various homework problems and labs. Be sure you understand and are able to remember every vocabulary item that is in boldface.
Be sure to bring a pencil and calculator.
You should be able to
- Calculate the frequency, angular frequency, or period of a pendulum or mass on a spring, or calculate properties of those oscillators given the frequency, angular frequency, or period.
- Solve for any one of distance, velocity or time for a wave, given the other two.
- Solve for any one of wavelength, frequency or velocity, given the other two.
- Calculate the period of a wave if given the frequency, and vice versa.
- Calculate the wavenumber of a wave if given the wavelength, and vice versa.
- Identify the parts of the ear on diagrams, and know the functions of the various parts.
- Know the different types of waves and an example of each.
- Understand the importance of the decibel in measuring sound intensity.
- Describe constructive and destructive interference, and examples of interference such as beats, standing waves, and shocks.
- Calculate the lengths of pipes needed to produce a specified fundamental frequency.
- Describe qualitatively, or calculate, the Doppler Effect and how the relative motion of a wave source and observer affects the frequency or wavelength observed.
You are expected to have memorized the speed of sound in air and the strength of gravity on Earth. Be sure you understand the boldfaced vocabulary words in both the textbook and supplementary readings. Go over the labs, and use the "practice another version" in WebAssign for additional practice beyond the problems below.
You may also want to review essential skills such as unit conversions and SI prefixes. I will freely use units such as msec or μm without explanation. I will give you any conversion factors between SI and non-SI units.
Relevant Equations: You are expected to have these equations memorized, to be able to solve any equation for any of the variables in it, and to use the equation appropriately for calculations.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Practice Problems Assume all given numbers are valid to 3 sigfigs.
Practice Problems
1. As a fire truck (with siren blaring) is coming towards
you, the __________ is steadily increasing and the ________ is constant.
The instant
the truck passes you, the __________ drops. As the truck moves away,
the
__________ gradually decreases.
FILL IN EACH BLANK WITH ONE OF THESE WORDS (yes, you can use a
word more than once)
PERIOD FREQUENCY WAVELENGTH VELOCITY LOUDNESS
2. Fill in the missing labels on this diagram of the ear.
3. How much time would it take a sound (assuming it were loud enough) to travel completely around Earth? (Earth's circumference is 40,000 km.)
4. Describe the purpose of the following parts of the ear:
(a) cochlea
(b) eustachian tube
(c) auditory nerve
5. If you listen to loud sounds, what part of the ear gets damaged? Be specific.
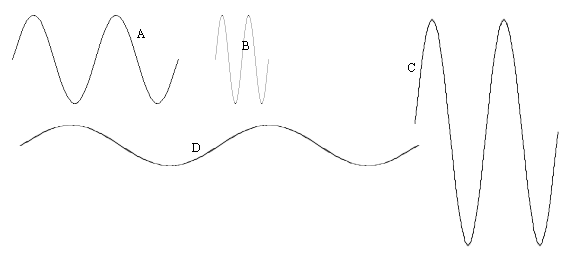
6. Here are several waves.
(a) Which one has the greatest amplitude?
(b) Which one has the greatest wavelength?
(c) Which wave above has the shortest wavelength?
7. (a) Measure the wavelength of wave D. What is it?
(b)
If wave D were a light wave, what would be its frequency?
(c) What would
be its period?
8. You have two tuning forks, one with a frequency of 512 Hz and the other with frequency of 520 Hz.
(a) Which tuning fork's tone has the greater period?
(b) What is the beat frequency you hear if you strike both forks simultaneously?
9. How many times louder is the "threshold of pain" than the "threshold of hearing"? (See the decibel chart on the Sound page.)
10. How long would a flute (open at both ends) have to be, in order for its fundamental frequency to be 20 kHz, the highest sound (young) humans can typically hear? What are the frequencies of the first two harmonics?
11. (a) The lowest note on a piano keyboard is 27.5 Hz. What is the wavelength of that sound?
(b) The highest note on a piano keyboard is 4186 Hz. What is its wavelength?
12. A particular organ pipe produces a fundamental frequency of 1000 Hz, with harmonics at 3 kHz, 5 kHz, and 7 kHz. How long is the pipe? Is it open at both ends, closed at both ends, or open at one end?
13. If one sound is 1,000,000 times louder than another, how many decibels higher is the loud sound compared to the quieter sound?
14. One tuning fork has a frequency of 512 Hz. What other frequency would produce a beat frequency of 15 Hz?
15. A Wikipedia article about organs includes this sentence: “Open pipes are open-ended. An open pipe producing middle C is about two feet in length.” Is the Wikipedia author correct? To find out, calculate the length of a pipe, open at both ends, that produces a fundamental frequency of 261.6 Hz (a middle C). Is that about two feet? (Remember, 1 inch is 2.54 cm.)
16. Miscellaneous short-answer questions:
"Pitch" is another word for the ___________ of a sound.
What are the names of the three tiny bones that connect your eardrum to the oval window?
The frequency of a fire truck siren coming towards you is ____________ than the frequency if the truck weren't moving.
You go to the theatre to see a play. At your seat, you notice that the sound is strangely muted and quiet. You are sitting at a place of _______ interference of the sound waves. This place is called a ________.
17. How long would a pendulum have to be in order for its period to be exactly one minute.
18. You have a spring that is 25 cm long. You hang it vertically, suspended from one end, and attach a 5-pound weight from the bottom. Without oscillating, the spring stretches so it is now 39 cm long. Now, you remove the 5-pound weight and put a 0.5 kg mass on the spring instead. You pul the spring down and release. What are the frequency and period of the resulting oscillations. [NOTE: 1 pound is 4.44 Newtons.]
19. You have a pendulum of a certain length and you measure its period. If now you make the pendulum n times longer, will the period be longer, shorter, or unchanged. What is the ratio of the new period to the old period?
20. If a set of hearing protectors say they decrease the sound loudness by 25 dB, how many times quieter (or less loud) do the hearing protectors make sound?