Learning Measurement: Waves & Acoustics
Goals and Review ANSWERS

Practice Problems

1. As a fire truck (with siren blaring) is coming towards you, the _loudness_ is steadily increasing and the _frequency_ is constant. The instant the truck passes you, the _frequency_ drops. As the truck moves away, the _loudness_ gradually decreases.

2. Fill in the missing labels on this diagram of the ear.

a. pinna    b. cochlea    c. auditory nerves   d. Eustachian tube    e. eardrum    f. ear canal

3. How much time would it take a sound (assuming it were loud enough) to travel completely around the Earth?

Time = distance / velocity = 40000 km/0.343 km/sec = 1.2x10⁵ sec = 32 hours

4. Describe the purpose of the following parts of the ear:

(a) cochlea Detects sound waves and converts them to nerve impulses that get sent to the brain. Contains nerve cells with hairs projecting into fluid on its inside. Sound waves in the fluid (transmitted there by the eardrum to the hammer, anvil and stirrup to the oval window into the fluid) move the hair cells, causing the cells to send signals to the brain.
(b) Eustachian tube  Allows the air pressure inside the middle ear to equalize with the outside atmospheric pressure, by allowing air to escape or enter.
(c) auditory nerve Transmits infomation about the detected sound waves from the cochlea to the brain, where sound is perceived.

5. If you listen to loud sounds, what part of the ear gets damaged? Be specific. The hair cells in the cochlea

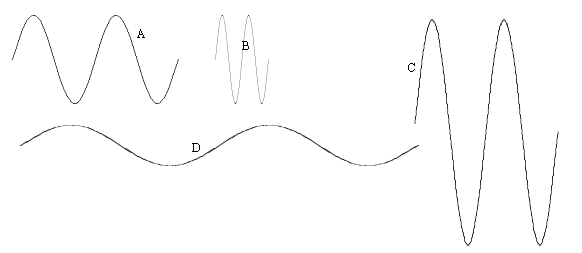
6. Here are several waves.

(a) Which one has the greatest amplitude? C
(b) Which one has the greatest wavelength? D
(c) Which wave above has the shortest wavelength? B

7. (a) Measure the wavelength of wave D. What is it?

Put a ruler down on the screen or paper and measure. Your answers will vary depending on screen, zoom, etc.

    (b) If wave D were a light wave (the speed of which is 3.00x10⁸ m/sec), what would be its frequency?

f=(speed of light)/(wavelength from part a). Be sure the units are consistent!

    (c) What would be its period? The reciprocal of your answer b.

8. You have two tuning forks, one with a frequency of 512 Hz and the other with frequency of 520 Hz.

(a) Which tuning fork's tone has the greater period? the 512 Hz tuning fork (period and frequency are inversely proportional)
(b) What is the beat frequency you hear if you strike both forks simultaneously? 8 Hz

9. How many times louder is the "threshold of pain" than the "threshold of hearing"? (See the decibel chart on the Sound page.) a trillion times (10¹²)

10. How long would a flute (open at both ends) have to be, in order for its fundamental frequency to be 20 kHz, the highest sound (young) humans can typically hear? About 9 mm. What are the frequencies of the first two harmonics? 40 kHz, 60 kHz

11. (a) The lowest note on a piano keyboard is 27.5 Hz. What is the wavelength of that sound? 12.5 m

       (b) The highest note on a piano keyboard is 4186 Hz. What is its wavelength? 8.2 cm

12. A particular organ pipe produces a fundamental frequency of 1000 Hz, with harmonics at 3 kHz, 5 kHz, and 7 kHz. How long is the pipe? Is it open at both ends, closed at both ends, or open at one end? We know it's open at only one end because the overtones are only the odd multiples of the fundamental frequency. The pipe is 8.6 cm long.

13. If one sound is 5,000 times louder than another (as measured in W/m²), how many decibels higher is the loud sound compared to the quieter sound? 37 dB

14. One tuning fork has a frequency of 512 Hz. What other frequency would produce a beat frequency of 15 Hz? Two answers: 497 Hz or 527 Hz.

15. A Wikipedia article about organs includes this sentence: “Open pipes are open-ended. An open pipe producing middle C is about two feet in length.” Is the Wikipedia author correct? To find out, calculate the length of a pipe, open at both ends, that produces a fundamental frequency of 261.6 Hz (a middle C). Is that about two feet? (Remember, 1 inch is 2.54 cm.) L = 0.65m = 26 inches. Yes, that's roughly 2 feet.

16. Miscellaneous short-answer questions:

"Pitch" is another word for the _frequency_ of a sound.

What are the names of the three tiny bones that connect your eardrum to the oval window? hammer, anvil, stirrup

The frequency of a fire truck siren coming towards you is ___higher__ than the frequency if the truck weren't moving.

You go to the theatre to see a play. At your seat, you notice that the sound is strangely muted and quiet. You are sitting at a place of _destructive_ interference of the sound waves. This place is called a __node__.

17. How long would a pendulum have to be in order for its period to be exactly one minute. About 890 m

18. You have a spring that is 25 cm long. You hang it vertically, suspended from one end, and attach a 5-pound weight [which is 22.2 Newtons] from the bottom. Without oscillating, the spring stretches so it is now 39 cm long. Now, you remove the 5-pound weight and put a 0.5 kg mass on the spring instead. You pul the spring down and release. What are the frequency and period of the resulting oscillations. First, find the spring constant,k. F_spring=k·Δx, so k=F_spring/Δx = 22.2N/0.14m = 159 N/m. Now that we have k, we can calculate the period. T = 0.35 sec

19. You have a pendulum of a certain length and you measure its period. If now you make the pendulum n times longer, will the period be longer, shorter, or unchanged. What is the ratio of the new period to the old period? Longer, by a factor (ratio) of square root of n.

20. If a set of hearing protectors say they decrease the sound loudness by 25 dB, how many times quieter (or less loud) do the hearing protectors make sound? 316 times quieters (i.e. the sound entering the ears is reduced to only 1/316th of its intensity.)