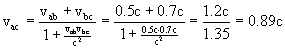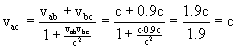Special Relativity
The Looming Crisis Towards the end of the nineteenth century, and in the beginning of the twentieth, a series of phenomena were discovered that could not be explained by the physics we have so far discussed. Physicists were forced to radically alter their perception of how the Universe works. Most didn’t like it, but given the tenets of science, they had no choice. These new phenomena were discovered as developing technology made new experiments possible. The most influential of these experiments was conducted by Michelson and Morley.
Maxwell said light is an EM wave traveling at a speed of c=3.00x108 m/sec, relative to the ether. The ether was the medium, which (it was thought) was necessary to have, just as water waves require water and sound requires air. The ether, since we don’t really notice it, had therefore to be relatively invisible, massless, but also very strong to make the light travel as fast as it does. But it has to be detectable somehow, if we’re careful and clever enough. And here’s how we’ll do it, went the reasoning:
Newton's second law applies only in an inertial reference frame (or just "frame") i.e. a coordinate system moving at a constant velocity (with no acceleration), because FNET=ma makes no reference to a velocity, only to a change in velocity. So, for example, on an airplane moving at 600 mph Newton's laws work just as if the plane weren't moving at all. If you drop a ball, it falls at your feet, just as it would on the ground. On the other hand, if the plane accelerates, the inertia of the ball will make it move relative to the plane: if the plane slows down while the ball is falling, the ball will land forward. Furthermore, there is no apparent force on the ball — to the observer on the plane the ball appears to have accelerated with no force causing that acceleration, violating FNET=ma.
This idea — that all the laws of nature apply in all inertial reference frames — is called the principle of relativity. A by-product of this is that we can’t determine the absolute velocity of the frame by any experiment: since all the laws operate exactly the same, they can't be used to distinguish between two frames moving with a constant velocity relative to each other. This concept played a role in the eventual acceptance of the Copernican model of the solar system. Opponents’ of Copernicus had argued that, if Earth was spinning and moving, a falling object would appear to curve. To counter this argument, Galileo is said to have dropped a ball from the mast of a moving ship. The ball landed at the base of the mast, not behind the mast as the adherents of Aristotelian physics believed.
Example: Passenger walking backwards on airplane. Really a vector addition.
Example: swimming at the beach, airplanes landing in crosswinds.
Later on, however, a problem developed: Maxwell's equations. Mathematically,
Maxwell's equations make a distinction between the case of a magnet moving
past a coil of wire and a wire moving past a stationary magnet. It happens
to work out that the equations yield the same result in both cases: a
certain amount of current flows in the wire. This seemed like a great
coincidence. Also, when Maxwell derived his equations showing the motion
of an electromagnetic wave with velocity c, that velocity was with respect
to the ether. If Maxwell was right about the ether, IT could represent
THE inertial, absolute reference frame of the Universe, that everything
else could be measured with respect to. This was the holy grail of nineteenth-century
physics. We live on a planet that is rotating (at about 1700 km/hour)
which orbits the sun (at 30 km/sec), which orbits the Galaxy (at 250
km/sec or so), etc... To find the rest frame of the Universe would be
a momentous discovery.
Michelson-Morley Experiment (1887). Michelson and Morley wanted to detect the
motion of the Earth through the ether, by measuring the resulting ether "breeze".
The device they employed (the Michelson interferometer) uses the wavelength
of light as a measuring rod. Refer to the diagram.
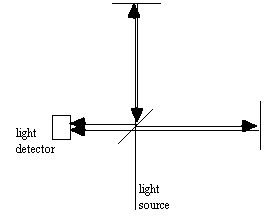
A ray of light from a light source strikes a half-silvered mirror at a 45° angle. Two beams emerge at right angles to each other, which then go on to strike two fully-reflective mirrors straight on. The two beams reconverge at the half-silvered mirror, and half of each beam ends up at a light detector, which in 1887 would have been a human eye. Because the two beams were originally split from one, they start out in phase. If we assume that both arms of the interferometer are the same length and that there is no ether breeze, the two beams should arrive at the "detector" still in phase. The beams constructively interfere and there is a bright spot. Now imagine that there is an ether breeze blowing to the right on the diagram. The light beam travelling parallel to the breeze effectively has a longer path to travel (even if the physical distances are identical). It therefore takes more time to take the trip, and is out-of-phase with the other beam when it reaches the detector.
Realistically, it was impossible for Michelson and Morley to make the two arms of their interferometer exactly the same length, but they didn't have to. Whatever lengths the arms have is fine, and the two beams combine and produce either a bright spot (total constructive interference) or a dark spot (totally destructive interference) or something in between. Now when the whole contraption is rotated, either by the experimenters or due to the rotation of the Earth, the relative phase of the two beams should change. The spot should have changed its brightness, either up or down. But nothing happened when Michelson and Morley did this. Their experiment was so sensitive (because the wavelength of light is so short) that they should have detected the flow of the ether past the earth. No such breeze was detected.
RATIONALIZATIONS
Michelson and Morley detected no ether breeze. How did they, and others, explain this? There were several ideas bandied about. Perhaps Copernicus was wrong, and the Earth really is stationary at the center of the Universe. But the evidence for the motion of the Earth was conclusive by this point, especially the parallax seen in the stars. Another idea: Maybe there was no ether, therefore there could be no breeze. But waves need a medium, so no one could accept this.
Another idea: Maybe there is an ether layer ‘sticking’ to the Earth’s surface, being dragged along because of a slight viscosity. This is similar to the surface layer on a wing or fan blade. (Ever notice how dust collects on fan blades, even when the fan has been in use? This is possible because the layer of air right next to the blade sticks to the blade and moves along with it. Therefore, any dust particle that lands on the blade surface does not get knocked off.) There’s a problem with this idea too: if the ether were viscous, the drag would sap kinetic energy from the Earth in its orbit, and the Earth would gradually be spiralling into the Sun. Clearly that isn’t happening.
Yet another possibility was suggested by FitzGerald and Lorentz. Perhaps the slight pressure of the ether breeze on the parallel arm of the interferometer was compressing it slightly. If that arm were shortened by a factor of
(where c is the speed of light relative to the ether and v is the speed of the Earth relative to the ether) then the time for light to traverse both arms of the interferometer would once again be the same. This idea was called Lorentz Contraction. But it sure seemed odd that the ether would compress the interferometer just the right length to make detecting the ether impossible. And it didn't seem to matter what materials the interferometer was made of, they were all compressed by that same numerical factor. And if the ether exerted that kind of pressure on the interferometer, we again run into the paradox that this phenomenon has no effect on the stability of earth's orbit around the Sun.
Activities & Practice
to do as you read
See Al's Relativistic Adventures, at http://www.onestick.com/relativity/
EINSTEIN
1905 was a good year for Albert Einstein. In that year, he published five scientific
papers, three of which were fundamental and revolutionary. One of these papers
was "On the Electrodynamics of Moving Bodies", and found a way of
explaining the negative results of the Michelson-Morley experiment. This was
a good thing, but in the process Einstein showed that some of the assumptions
underlying Newtonian physics were not valid. The result was Special Relativity.
What drove Einstein in the particular direction he took? We've already discussed one of his motivations — the Michelson-Morley experiment. Einstein was dissatisfied with the various explanations for the failure to detect the ether breeze. The Lorentz contraction idea, especially, seemed too post hoc and (recall our previous discussion, that any scientific hypothesis must be falsifiable) unscientific. Because there seemed to be no way to detect the ether, Einstein felt it best to not believe in it. He was a bit like the boy who cried out that the emperor wasn't wearing any clothes. As Einstein reminisced in 1920, "The laws [Maxwell's Equations] were clear and simple, their mechanical interpretations clumsy and contradictory." Once he made that step, the consequences of the Michelson-Morley experiment are this...
Postulate #1: Universal Speed of Light. The speed of light in a vacuum is the same as measured by all observers, regardless of any motion of the light source or the observer.
I have only hinted at the second of Einstein's motivations. Earlier, we saw that a charged particle moving past a magnetic field experiences a force, and also that a moving (or changing) magnetic field exerts a force on a stationary charge. As Maxwell's Equations were written, there is a distinct difference (in mathematical form) between these two cases: moving charge or moving field. In one case the electric field exerts the force, in the other case the magnetic field does.
This presupposes that there is some unique reference frame in the universe that defines rest. Despite the difference in form, Maxwell's equations predict the same force on a charge, regardless of whether the charge is moving or the field — and despite the fact that neither is in the rest frame of the ether. This seemed to be a remarkable coincidence. Mechanics does not require a special coordinate system: Newton's laws work equally well on moving ships, or cars — just so long as they are moving at a uniform speed. This is convenient, because we have no knowledge of what that universal rest frame is. (Newton himself thought that it must exist.) To Einstein, these convenient and coincidental facts all pointed in the same direction:
Postulate #2: ALL the laws of physics apply in all inertial reference frames. Not just mechanics, but E&M also should not make reference to absolute motion.
These two postulates formed the foundations of special relativity. They probably don't seem all that remarkable, at first glance. The conseqences of these statements, however, can be downright bizarre...
Gedanken Experiment #1: The Relativity of Simultaneity
Einstein was a theorist, not a laboratory physicist. His lab was his pencil and paper. Nevertheless, he liked to couch his arguments in experimental terms. He invented many thought experiments (gedankenexperimenten, in German) to derive and explain the consequences of his postulates. Of course, in the end, the results of Special Relativity must be tested with real-world experiments. We will look at those tests later on.
First, we must design the laboratory in which to conduct our thought
experiments. Because this is only an imaginary lab, money is no object.
Our equipment is simple: only our eyes, rulers, and clocks — but
we need lots of them. We also need a lot of assistants, whom we will
call observers. We will put down the rulers, establishing
a coordinate system, and also a clock at every point in space. Together,
these coordinates and clocks constitute a reference frame,
or simply "frame" for short. We can make a
duplicate set of coordinates and clocks, and this duplicate set can be
set in motion (at constant velocity) relative to the first frame. The
first frame is our lab frame; the other is the moving
frame. Any event can be described by its coordinates in space
(x,y,z) and time (t).
Now, let's do our first gedanken experiment. Imagine a freight car that is
moving along some railroad tracks. The car is the moving frame; the ground
is the lab frame. Imagine further that there is, for some reason unbeknownst
to us, a flashbulb hanging in the center of the freight car, as well as one
of our assistants. The bulb flashes. What does the observer on the car observe?
The flash hits the rear and front walls of the car simultaneously. This is
obvious, right? The forward-going and rearward-going light rays, after all,
are going the same distance at the same speed, so of course they will reach
the ends of the car at the same time.
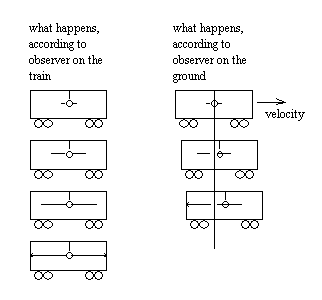
What does an observer on the ground (the lab frame) see? The forward and rearward-moving rays move with identical speed. But to the lab frame observer, the car is moving forward. The rear wall is moving toward the flashbulb and the front wall is moving away, so of course the light hits the rear wall first. The two events (light hitting the front and rear walls) are not simultaneous, according to the observer in the lab frame.
So who's right? Are the events simultaneous or not? The answers to these questions are: 'They both are.' and 'It depends.' This paradox-like situation is known as the relativity of simultaneity. Note how all this hinges on Postulate #1. According to an observer on an express train passing the freight train, the light hits the boxcar's front wall first!
Note also that this result has nothing to do with effect of the light's travel time to the observer. Think about the observer on the train car. If this person is standing in the exact center of the car, as described before, she will see the front and rear walls light up simultaneously. But if she is standing closer to the front of the car, she will see the front wall light up slightly before the rear wall because, even though the flash hits both walls at the same time, it takes slightly less time for the reflected flash from the front wall to reach the observer's eyes. But the observer knows where she is standing, and can calculate that both walls were illuminated at the same time. I am making an important distinction between what is seen and what is observed. Observation implies that the time of an event has been corrected for any light-travel time between the observer and the event. Another way to avoid the light-travel-time error is to put observers and synchonized clocks everywhere in the frame. Our imaginary observers can write down the time of an event that happens right next to them, using the clock that is right next to them. There's no travel delay for the light from either the event or the clock, and all the observers can get together later and compare notes.
Gedanken Experiment #2: Time Dilation Now, let's conduct another thought experiment, being a little more mathematical this time. Consider vertical light propagation. Let's put a flashbulb on the ceiling of the freight car. How long does it take the light from the flashbulb to reach the floor? To the observer on the car, the time is
![]()
where h is the height of the bulb above the floor of the car, and the
prime indicates an observation from the car. This is the so-called proper
time, measured in the rest frame of the flashbulb and car.
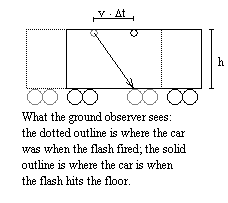
To the observer on the ground, the light takes an amount of time Δt, the improper time. The lack of a prime (') indicates a measurement from the ground. During this time, the car travels forward a distance v· Δt. The light ray that hits the floor under the flashbulb must, therefore, travel a greater distance, the hypotenuse of a right triangle with legs of length h and v· Δt. Using the Pythagorean Theorem, that distance is
![]() , so the improper time
is
, so the improper time
is ![]() . Solving for Δt,
we get
. Solving for Δt,
we get
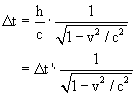
The term ![]() is replaced with
a new symbol, γ, because we'll be using it
often. With this definition, the result of this thought experiment is...
is replaced with
a new symbol, γ, because we'll be using it
often. With this definition, the result of this thought experiment is...
![]()
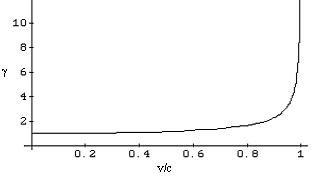
What does this derivation show? Looking at γ, you should be able to see that it is always greater than or equal to 1: if v is not zero, then the denominator is less than one, and therefore γ is greater than 1. So the time interval measured by the ground observer is greater than the time interval measured by the observer on the car, i.e. moving clocks run slow. This is called time dilation.
In the limit of slow speeds, γapproaches one; in
the high-speed limit, γ grows without bound as
v gets closer to c. In other words, at the speed of light γ is
infinitely large. A graph of γ as a function of
v/c is shown here.
The clock in our thought experiment is an unusual design. Most real clocks
use a vibrating quartz crystal, pendulum or spring to keep time. These things
all vibrate at a fixed rate. Nevertheless, the result of our gedanken experiment
has nothing to do with the mechanism of the clock. The clocks run slow because
time itself is running slow. If this weren’t true, consider the paradox
of placing a quartz clock, say, next to our light-tick clock. All observers
must agree on whether they read the same time or not. They may disagree on
the rate those two clocks run, but they do run in sych with each other. Time
dilation has to do with the failure of simultaneity, therefore is not dependent
on the mechanism of the clocks used. Make a clock from the light ray set-up,
and another with a quartz crystal, pendulum, etc., and if they’re next
to each other and moving together, all observers will agree that they are
counting the same time.
Does time dilation violate the first relativity postulate? The ground observer
O says the train clocks run slow, and the train observer says the same thing
about the ground clocks! Both are correct, but they are measuring different
things. The train (O’) observer is comparing two of her clocks with one
on the ground; the ground observer O is comparing two of his own clocks with
one on the train. Each observer uses two clocks in her/his own frame because
there is no problem synchronizing those clocks. But as viewed from the other
frame those two ‘synchronized’ clocks won’t be. The other
observer concludes that his counterpart is stupid for measuring his time with
two clocks that aren’t even synchronized!
EXAMPLE: Alice and Abe are fraternal twins. Alice is an astronaut, Abe is an accountant, and they are both 30 years old. Alice takes off on a voyage at (12/13)c. After five years (on her watch) she turns around and comes back, which takes another 5 years. Therefore she is 10 years older than when he started, i.e. 40. Abe, meanwhile, has been on the Earth, accounting. He aged
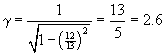
times faster. Twenty-six years has passed for him, so when Alice returns her brother is 56: they are no longer the same age.
This particular problem is known as the twin paradox. As seen
by the travelling twin, Alice, it’s the earth (with Abe on it) that flies
off at (12/13)c. So shouldn't he be aging slower than her? The symmetry between
their two situations is broken by the fact that the travelling twin is not
in an inertial reference frame for the whole trip. Alice accelerates, whereas
Abe does not.
This is weird stuff – but wait, there's more!
Gedanken Experiment #3: Lorentz Contraction Let's do another (our last) thought experiment. Consider light propagating parallel to the motion now. Let's place a mirror at one end of the boxcar, and a flashbulb at the other. How long will it take the light flash to make the round trip? Since light travels at a fixed speed, we can use the travel time of the light to calculate the length of the car. If the length of the car (as measured by the observer on the car) is Δx', the proper time for the light to make a back-and-forth trip is Δt'=2Δx'/c. As measured from the ground, it's going to take a different amount of time to travel forward in the car than to travel backwards, because the front wall of the car is moving away from the light as it moves forward, and the rear wall moves forward to meet the reflected flash as it travels backwards. The times for the forward and backwards legs of the trip are, respectively,
![]()
The time intervals appear on both sides of these two equations, so we have to solve them, getting the time intervals on the left-hand side of each equation by themselves:
![]()
The total round-trip time
![]() .
.
The two time intervals are related by the time dilation equation, ![]() .
Plugging our expressions for Δt and Δt'
into this equation gives us a relation between Δx
and Δx':
.
Plugging our expressions for Δt and Δt'
into this equation gives us a relation between Δx
and Δx':
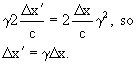
What does this say? Remember, γ is always greater
than 1, assuming that v>0. So what we have just proven is that moving objects
are shortened (but only along the direction they are moving.) This is called Lorentz
contraction. If you recall the pre-1905 attempts to explain the failure
of the Michelson-Morley experiment, Lorentz had proposed that the interferometer
arm parallel to the ether breeze was shortened by a factor of ![]() .
Einstein derived exactly the same numerical shortening, but the interpretation
is far different: an object is shorter because the space the object occupies
has contracted.
.
Einstein derived exactly the same numerical shortening, but the interpretation
is far different: an object is shorter because the space the object occupies
has contracted.
EXAMPLE: A rectangular spaceship at rest has dimensions 400 m by 300 m by 300
m. How fast must it move, and in what direction, so it appears cubical to
a stationary observer?
SOLUTION: The only way to make the spaceship cubical is to shrink the 400-meter-long
side to 300 meters in length. It must be shrunk to 75% of its rest length,
so gamma must be 4/3. At what velocity is gamma equal to 4/3?
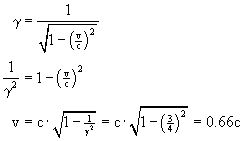
Here is another relativistic fable, the Barn-and-Ladder Paradox:
A farmer wants to put a ladder in the barn, but it’s too long. Having
heard about the Lorentz contraction on the farm report that morning, he decides
to run very fast with the ladder (shortening it), and have his son close the
door when he’s inside. The son says “But Dad, from your perspective
the barn will be shortened, not the ladder, so this procedure will only make
things worse as far as fitting the ladder in the barn.” Who's right?
They are both right! When we say ‘the ladder is in the barn’ that
means that at one instant of time both the front and rear ends of the ladder
are within the confines of the barn. But simultaneity depends on the observer.
There are two events of concern: (1) back end of ladder gets through door,
and (2) front end of ladder hits the far wall. Runner says (2) precedes (1),
whereas a stationary observer says (1) precedes (2). When it’s all over
and done, either it’s in or not, right? No, because to stop the ladder
it must accelerate (or decelerate, as it were). As it slows down, it expands
(as seen by the stationary observer), and in the end, either the ladder or
the wall is broken.
Einstein’s velocity addition rule. Imagine a
spaceship traveling at 0.5c relative to a planet. An astronaut with
a very good throwing arm hangs out an open window and throws a water
balloon
forward at
a speed
of 0.7c, relative to the ship. How fast is the balloon moving relative
to the planet? Using the usual rules of 1-dimensional vector addition,
you'd say the balloon was traveling at 1.2c, right? This is called
Galileo’s velocity addition rule, and can be
summarized as
where "a", "b", and "c" refer to three frames. In our imaginary example here, "a" is the balloon, "b" is the spaceship, and "c" is the planet.
vab is the velocity of the balloon relative to the ship,
vbc is the velocity of the ship relative to the planet,
vac is the velocity of the balloon relative to the planet.
But wait, that can't be right! Einstein said, and all experiments confirm, that nothing can travel faster than c. Galileo's rule must be wrong! Einstein instead proved that the correct rule is
Let's look at the behavior of this odd equation for a couple of situations. First, notice that the term
is practically zero for normal, everyday velocities (because c² is such a huge quantity). That makes the denominator
essentially equal to one. Einstein’s velocity addition rule for slow speeds is therefore, for all practical purposes, the same as Galileo’s. This is illustrated by the following example...
EXAMPLE: A person standing in a convertible traveling at exactly 30
mph relative to the ground throws a baseball forwards at exactly 30
mph, relative to the car. What is the ball’s velocity relative to the
ground?
SOLUTION: Galileo, of course, would say that the baseball is traveling at exactly
60 miles per hour. Actually, at first he'd ask what a baseball was, because
there were no baseballs in the seventeenth century. But then he would say that
the baseball thing was moving at 60 miles/hour.
Einstein gives a slightly different answer. To calculate it, we need to know
the speed of light in miles per hour; it's c=6.7x108 mph. Then
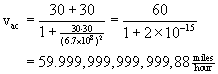
So you can see why we don't notice the difference between Einstein's velocity-addition
rule and Galileo's in our everyday lives.
Of course, it has to work out like that, because we know that Galileo's velocity-addition rule works in normal situations. What Einstein did was to make a small correction, a tweak, to the old rule. We will see this with quantum mechanics also: in the regimes of previous experience, the new rules should look very much like the old rules, because the old rules were previously known to be valid within the limits of measurement. This idea is called the Correspondence Principle, and we'll be discussing it again later on.
When one or
both of the velocities is not small compared to the speed of light, then
the predictions of Einstein's velocity-addition rule differ
radically from the galilean rule...
EXAMPLE: A person standing in a convertible traveling at exactly 0.5c
relative to the ground throws a baseball forwards at exactly 0.7c, relative
to the car. What is the ball’s velocity relative to the ground?
SOLUTION: These are the same numbers as mentioned previously. Let's
see what really happens...
The ball isn't even moving at the speed of light, much less 1.2c!
EXAMPLE: In fact, the structure of this equation forces vac to always
be less than, or at most equal to, the speed of light. Let's say this very
reckless
person, standing up in fast-moving convertibles, shines a flashlight forward
from a car moving at 90% of the speed of light. The light has velocity vab=c
relative to the car. How fast is the light beam moving according to the stationary
observer? Here's the calculation...
The observer, of course, sees light traveling at the speed of light, as the first postulate said. The velocity-addition rule was derived from that postulate, so we shouldn't be surprised that this is all consistent! But what this means is that nothing can move faster than c, as seen by any observer. That is, c is a universal speed limit.
Mass-Energy Equivalence: The last result of Einstein's Special Relativity that we will discuss here is this...
Energy itself has inertia. Remember, mass as "inertia" are essentially synonyms, so mass and energy can be considered two aspects of the same thing, a concept that physicists hyphenate as mass-energy.
We don't notice this effect in our everyday lives because the inertia (mass) associated with any typical amounts of energy is very, very small. The mass of a certain amount of energy is given by this equation:
which is more widely known in this form: E=mc²
If we say that energy is a form of mass, then mass must be a form of energy. An object's mass, it seems, is a very concentrated form of energy.
The object's mass when it is not moving is called its rest mass, m'. For a moving object, its kinetic energy contributes additional mass. Adding the mass of its KE to the object's rest mass yields its apparent mass, m.
m = γ·m'
So we can rewrite ![]() as
as ![]()
Experimental Confirmation. You can ask (indeed, you should ask) if any of these bizarre predictions of Einstein’s Special Relativity have been demonstrated with actual experiments conducted in the real world. After all, we don’t really have (yet) spaceships that can move near the speed of light, where time dilation, Lorentz contraction and Einstein's velocity-addition rule become obvious. So why should we believe all of this is anything more than numerology?
Let's look at time dilation first. Although we don't have the technology to send any large object near the speed of light, it's fairly easy to accelerate subatomic particles to such great speeds. Many subatomic particles are stable, but others, such as muons and neutral pions are unstable. In other words, they are radioactive, spontaneously disintegrating in a certain average time called the halflife, t1/2. For muons, t1/2=2.2x10-6 sec; for neutral pions it’s 8x10-17sec. These times were measured when the particles are at rest. When moving very fast in a particle accelerator, however, they last much longer as measured by scientists in the lab frame. There are also muons created naturally by the collision of primary cosmic rays with the atoms comprising the upper atmosphere. These muons move with speed very close to c, so the typical muon should travel c·t1/2 =660m before disintegrating. Most muons, in other words, should not survive long enough to make it to the ground from the height of approximately 20 kilometers where they are created. Because they are moving near the speed of light, however, many survive to reach the ground.
The photos above show the world's largest particle accelerator, the Large Electron-Positron (LEP) collider at CERN, which straddles the Swiss/French border near Geneva. The underground tunnel housing the collider is circular, with a circumference of 27 km. The lefthand photo is an aerial view of the city, with the tunnel path marked to give you a sense of its size. The circle of a smaller collider is also shown. The righthand photo, at the bottom, shows the actual pipe in which the particle beams travel. Air is pumped out of this pipe so the particles don't collide with air molecules. The blue object around the pipe is one of hundreds of electromagnets that accelerate and steer the beams. The hanging monorail is used by scientists and technicians to access all parts of the tunnel.
Particle accelerators provide another test of Special Relativity. The force needed to accelerate the charged particles in the accelerator is provided by powerful electromagnets. The magnetic fields are created by electric currents, which are of course controlled by humans. As the particles travel faster, their mass increases. This increased mass, in turn, requires increased currents in the electromagnets to speed up the particles more, and to provide the centripetal force needed to keep the particles moving in the large loop. Taking the mass increase into account is designed into the control systems when these particle accelerators are built. It simply wouldn't work if Einstein's mass-energy equivalence equation was wrong.
In 1971, J.C. Hafele and R.E. Keating of the U.S. Naval Observatory placed 4 cesium atomic clocks aboard commercial airliners on world-circling routes. Based on the airplanes' routes, flight times and velocities, they calculated how much the moving clocks should differ from the stationary clocks that did not go on the airplanes. This experiment was only possible using atomic clocks that can meaure time to an accuracy of nanoseconds. Within the measurement errors, the results of the experiment matched the predictions based on the equations we've discussed above. [The experiment also tested the predictions of General Relativity, which we'll discuss next.]
PROBLEMS. (Check the answers after having done the problems.)
In calculation questions, show all your work. Write all velocities
in terms of c, the speed of light.
1. Synchronized clocks are placed at regular intervals along the x-axis
of your rest frame, separated by 1 billion kilometers. When the clock
next to you reads midnight, what time do you see on the 60th clock down
the line. What time does that clock really read?
2. The lifetime of a muon at rest is 2.0 µsec. After this time it spontaneously disintegrates. If the muon is accelerated in a particle accelerator to a speed of 0.95c, how long will it survive?
3. (a) What is γ, in the limit of slow velocities?
(b) How about in the limit of v approaching c?
4. How fast, in terms of c, must you be going for the length of your spaceship to appear 1/2 its rest length? How fast for it to appear 1/10 the rest length? solution video
5. As some outlaws escape in their getaway car, which is moving at 3c/4
(relative to the ground), a cop shoots a bullet from her police car,
traveling at only c/2 (also relative to the ground). The muzzle velocity
(speed relative to the gun) of the bullet is c/3. According to Galileo,
does the bullet reach its target? According to Einstein? solution video
6. In the year 2066, Earth builds a 120m-long spaceship of (rest)
mass 1.00x106 kg. The ship takes off at 0.6c towards the star
Gliese 699, which is 6 lightyears from Earth.
(a) Calculate γ.
(b) What is the apparent mass of the moving spaceship?
(c) What is the length of the spaceship as measured by the Earth?
(d) What is the length of the spaceship as measured by an astronaut on
the spaceship?
(e) How much time does it take the ship to arrive at Gliese 699, according
to the astronaut?
(f) How long does it take the ship to arrive, according to Mission Control
back on Earth?
7. The star Alpha Centauri is 4 light years
from the Earth.
(a) If a spaceship flies off at 0.87c towards this star, what is γ?
(b) How long does
it take to get there, according to an astronaut on the ship?
(c) How long does
it take to get there, according to people on Earth?
(d)
When the
ship arrives the astronaut sends a radio signal back to Earth. How
long after the ship left does the signal arrive (according
to clocks
on Earth)?
8. A car with rest mass m’=1000 kg is moving at a speed of 0.1c.
(a) Calculate the kinetic energy of the car using the Newtonian expression
for KE.
(b) Using Einstein’s equation E=mc², calculate the mass equivalent
of that KE.
(c) What then is the total mass of the moving car, i.e. its mass plus the
mass of its KE?
(d) Show that the answer to (c) is the same as gotten by calculating
m=γm’.
9. Explain why it is fundamentally impossible for a spaceship (or an
electron in a particle accelerator) to reach or exceed the speed of light.
10. Suppose you are traveling in space and pass a rectangular landing
pad on a planet. Your spacecraft has a speed of 0.85c relative to the
planet
and moves
in a direction parallel to the length of the pad. While moving, you measure
the length of the pad to be 1800m and the width to be 1500m. What are
the dimensions of the pad according to the engineers and construction
workers
who built it? solution video
11. The total amount of energy consumed in the U.S. in 1988 is estimated
to have been about 8.4x1019J. One penny has a mass of 2.9
g. If we could convert mass completely to energy, how many pennies worth
of
energy did
the U.S. consume
in 1988? solution video
12. How fast does a spaceship need to go, so it is shrunk 1%? solution video
13. An airplane is moving with respect to Earth, at a speed of 250 m/sec.
How much time (as measured by clocks on the ground) will it take for
the airplane's
clock to fall behind 1.0 second? solution video
14. Sketch a graph of γ as a function of v.
15. (a) Calculate, in meters, how long a light-year is.
(b) The diameter of the Earth is roughly 12800 km. How many Earth diameters
is a light-year?
16. The USS Enterprise is in a battle with a Romulan starship. The Enterprise
is moving at 0.9 c towards the Romulan ship, and fires a torpedo with
a speed of 0.7c (relative to the Enterprise). How fast is the torpedo
coming
at the
Romulan ship, according to the Romulans? solution video
17. What is the Correspondence Principle?
18. A human being who lives about 72 years (a typical lifetime) will
expend approximately 3x1011J maintaining basic metabolism
as well as a normal activity level. We get this energy by eating and
digesting
a lot
of
food during those
72 years. If we had stomachs that were able to convert food directly
and completely into energy, how many kilograms of food would an average
person
have to consume
in their lifetime? solution video
19. (a) The slowing of time in a moving frame is called...
(b) The shrinking of a moving object is called...