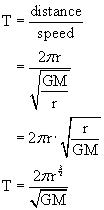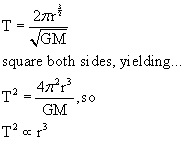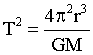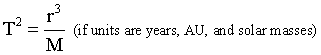Orbits

Way #1 On Earth, if you drop an object, how far does it fall in one second? If you said 4.9 meters, good! (Remember, d=½gt².) Recall also that how far an object falls vertically does not depend on how fast it is moving horizontally. For example, if you were to throw an object at 100 meters per second horizontally, it would still fall downwards 4.9 meters in the first second. What if you threw the object so fast horizontally that in one second it had moved so far to the side that the surface of the Earth would have curved 4.9 meters down? In that case, even though the object is falling, it wouldn't be any closer to the ground.

How fast is that speed? Consider a line tangent to a circle of radius 6378 km, the radius of the Earth. How big does Δx have to be, for Δy to be 4.9 meters?

Need a hint? Use the Pythagorean Theorem.

So a speed of 8 km/sec will keep an object in orbit around the Earth, if launched just above the surface. Of course, that's awfully fast. Any object moving that fast through the lower, thicker part of the atmosphere would burst into flames from friction with the air. That's why rockets are launched vertically: they need to get high up, above most of the atmosphere, and the shortest path out of the atmosphere is straight up. Once above the atmosphere, though, it's the horizontal velocity that keeps a satellite in orbit.

Activities & Practice
to do as you read

1. Go this Newton’s Mountain simulation applet http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=398.0

Answer these questions:

(a) What is the smallest initial speed that can create a closed orbit?
(b) If the initial speed is greater than the minimum needed, what does the orbit look like?

2. Go to http://www.arachnoid.com/gravitation/ and/or http://phet.colorado.edu/sims/my-solar-system/my-solar-system_en.html. Play. No written response needed.

3. Countries with space launch capability almost always launch their satellites so they orbit Earth in the eastward direction. Furthermore, these countries put their launch facilities as close to the equator as possible. For instance, the primary U.S. launch site is Cape Canaveral, Florida. The Soviet Union built its spaceport in a southern republic, Kazakhstan, and to this day Russia uses the same launch facility, leased from the independent Kazakhstan. The European Space Agency launches its rockets from Kourou, French Guiana, on the northern coast of South America, at only 5° North of the equator. So, here's my question: why do countries launch rockets to the east, and from as close to the equator as possible?

4. Convert the speed of 8 km/sec into (a) miles/sec, (b) miles/hour, and (c) Mach number. (The "Mach number" is the ratio of the speed to the speed of sound, which is about 340 m/sec or 750 miles per hour.) Use the factor-label method.

Videos:

http://www.youtube.com/watch?v=VDu9z4SCTmc&feature=related

http://www.youtube.com/watch?v=YxRCyokN3g8&NR=1

http://www.youtube.com/watch?v=vPQvTgD2quQ

Way #2 For a satellite moving in a circular orbit, what is providing the centripetal force keeping it moving in a circle? Yep, that’s right — gravity. So, if we call the mass of the planet M, the mass of the satellite m, and the radius of the orbit r, then the force of gravity between them is

Notice that the bigger the radius of the orbit, the slower the speed is. The speed is inversely proportional to the square root of the orbit radius: for example, doubling the radius will decrease the speed by a ratio of √2 = 1.41.

5. Use the equation at left to calculate the speed of the Moon, which is in a nearly-circular orbit around Earth at an average distance of 385,000 km. The mass of the Earth is M=5.98x10²⁴ kg. Solution video

6. The Earth goes around the Sun in a nearly-circular orbit of radius of 150 million kilometers, taking one year to complete an orbit. (a) From this known radius and time, calculate the velocity of Earth in its orbit. (b) Use your result and the equation at left to calculate the mass of the Sun. Solution video

Escape Velocity The above result is the velocity needed for a circular orbit at a distance r. If the velocity is greater than the required velocity, then the satellite will climb to a higher height. As it climbs it will slow and eventually stop climbing and then descend again, forming a closed ellipse. If it is moving fast enough, however, it will never stop climbing, but instead will fly away forever. The speed needed to do that is called the escape velocity. I'm not proving it here, but it turns out that the escape speed at a particular orbit radius r is √2 times the speed needed for a circular orbit of that radius.

7. Calculate the escape velocity from the surface of the Earth. SOLUTION

8. Listen to this podcast,called "Escape!", from WNYC's Radiolab. Actually, just listen to the middle of the three stories, which is about Newton, gravity and orbits. It starts at 27:10, going to 48:00.

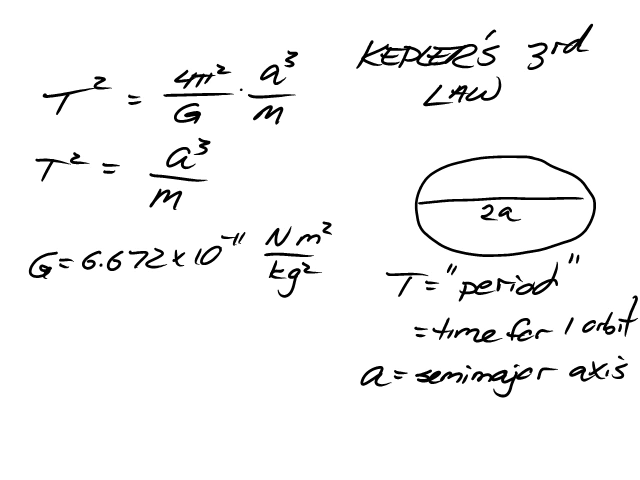
The Period of an Orbit

The time needed to complete a single orbit is called the period, T. The larger the orbit, the longer the period, for two reasons:

• For orbits of larger radius, the circumference is also larger. This is obvious.
• For orbits of larger radius, the speed is slower. This is not obvious, but was derived a few paragraphs above.

Exactly how much time does it take to complete an orbit? If the orbit is circular (and therefore the satellite's speed is not changing), the calculation is fairly simple. Recall that, for constant speed, the time is equal to the distance divided by the speed, t=d/v. For a circular orbit, the distance traveled is the circumference of the circle, 2πr...

You can use the above equation to directly calculate the period of a circular orbit, but you may find it easier to just calculate the speed (=circumference/period) first and then find the period (=distance/speed). The above derivation does allow us to do something interesting, though. Let's square the whole equation, and see what happens...

That last result you may recognize as Kepler's Third Law: the square of a planet's orbital period is directly proportional to the cube of the orbit's semi-major axis. (The semi-major axis is half the long dimension of an ellipse; for a circle, it's equal to the radius.) Johannes Kepler discovered this law in 1605 by analyzing massive amounts of planetary observation data collected by Tycho Brahe, who had died a few years earlier. This was 60-plus years before Newton's discoveries about gravity. Kepler didn't know why the period squared was proportional to the radius cubed. Newton was able to explain why: it's a consequence of the force of gravity being inversely proportional to the distance squared, as shown in the above derivations.

One last thing...let's look at the full equation for the period (squared) again.

The combination 4π²/G is just a constant. If we chose different unit, instead of meters, kilograms and seconds, the value of that constant would be different. In fact, we can choose units to make G equal 4π², and thus 4π²/G to equal 1. We can do this by choosing our distance unit to be the AU, mass unit to be the Sun's mass, and time unit to be a year. This is because the Earth's orbital period is 1 year, at a distance of 1 AU from a 1-solar-mass star. Expressed in these units, Kepler's Third Law becomes this...

Here's a video explaining this in greater detail.

Additional Activities & Practice

9. Calculate the period of a Space Shuttle orbiting Earth at a typical altitude of 250 km. Assume that you know the mass of the Earth is M=5.98x10²⁴ kg. (Be careful: r in the equation is the distance from the center of Earth, not the altitude.) SOLUTION

10. If a satellite is at the correct distance from the Earth, its orbital period will be 24 hours. Such an orbit is called a geosynchronous orbit, because the orbit is synchronized with the spin of the planet. (Geos is "earth" in Greek.) From the ground, a satellite in a geosynchronous orbit above the equator will appear to hang motionless in the sky, in the same spot all the time. Satellites below geosynchronous altitude (like Space Shuttles and the International Space Station, "rise" in the West and set in the East; satellites above geosynchronous altitude (like the Moon) rise in the East and set in the West, just like the Sun and stars. Geosynchronous orbits are typically used for communications satellites, so satellite dish antennas on the ground can simply be aimed at the right spot in the sky; the antenna doesn't need to find and move to track the satellite.

What radius orbit around the Earth will result in an orbital period equal to 24 hours? Step-by-step...

(a) Solve the period equation for r.

(b) Use the result of (a) to calculate the radius of the orbit. Assume that you know the mass of the Earth is M=5.98x10²⁴ kg. (Hint: be sure the period is in seconds. Keep track of the units!) Convert your final answer into km.

(c) How high is that above the surface, in km. How many Earth diameters is that?

SOLUTION

11. What is the radius of a synchronous orbit around Mars? (You will need to look up Mars' mass and rotational period.) Compare your result to the orbital radii of Mars' two moons, Phobos and Deimos. SOLUTION

12. SPREADSHEET: Create a spreadsheet that calculates the speeds and orbital periods of the planets in their orbits around the Sun. The mass of the star, M, and the universal gravitational constant, G, should be input cells near the top. M_Sun=2.0x10³⁰ kg. Below those, have columns for the planets' names and their orbit radii that you look up. Use astronomical units (1 AU = 150 million km, the average distance between Earth and the Sun.) To the right, have columns with the calculated speeds and periods. Speeds should be in km/sec and periods in years. Lastly, make two graphs, of speed and period as functions of the orbit radius.

[After you've attempted this problem, check your results against this screenshot. Keep in mind that the order of your calculations or the exact layout on the sheet may be different. That's OK. The numerical values of the final results, and the shapes of the graphs, though, should be the same.]

13. Corot-7b is a planet discovered in 2008, orbiting a type K0 main-sequence star. Type K0 stars have a mass of 0.93 M_Sun, and radius about 0.87 R_Sun. It was discovered by the transit method: from the viewpoint of the Earth, the planet happens to pass in front of the star, causing the brightness of the star to drop a little. These are very difficult measurements to make. In the case of Corot-7b, it blocks only 0.0335% of the star's light. A star's brightness can vary by that much even without a planet, by "starspots", for example. The presence of a planet can only be confirmed for sure if the transits repeat with a regular period. Corot-7b's orbital period is 20 hours 29 minutes 9.7 seconds.

(a) What is the distance of Corot-7b from its star, in AU?
(b) What is the diameter of Corot-7b, in km? How big is that, compared to Earth?

14. The Sun rotates once every 25 days at its equator. (Because the Sun is not solid, different latitudes can and do rotate with somewhat different periods, but we're ignoring that here.)

(a) What is the radius, in AU, of a "heliosynchronous" orbit?
(b) Sketch a diagram of the Sun and Mercury, to scale, indicating where the heliosynchronous distance is.

A few facts you need: the Sun's mass is 2.0x10³⁰ kg, 1 AU is 150 million km, the radius of Mercury's orbit  is 0.39 AU, and the radius of the Sun itself is 700,000 km.

SOLUTION