Telescopes
Introduction The basic idea of a telescope is simple: take light rays from an object and converge them to form an image. This image is usually called the prime focus image, and can be formed by either a convex lens or a concave mirror.
Activities & Practice
to do as you read
Refractors Telescopes that use a lens to form
the prime focus image are called refractors. The
prime focus
image can then
be examined in different ways: looked at directly with the eye, looked
at with an eyepiece, focused onto photographic film or a CCD detector,
or sent into a spectrograph.

A typical refractor consists of only two lenses, both converging. The big one
is called the objective: it collects the light and forms the prime focus image.
The bigger the area of the objective, the more light it collects and the brighter
the image will be. In other words, bigger objectives allow you to see fainter
objects. The prime focus image is usually rather small, so we use a magnifying
glass (called the eyepiece) to look at it.
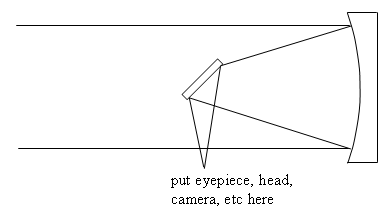
Reflectors Telescopes that use a concave mirror to form the prime focus image are called reflectors. These are a little more complicated than refractors, because the prime focus image is on the same side of the mirror as the object. Any camera, spectroscope or eyepiece (and head!) you put there to look at the prime focus image will block light from getting to the mirror. There are several solutions to this head-in-the-way problem...
The first solution, invented by Isaac Newton in 1670, is to place a flat mirror at 45° to the light beam reflected by the big mirror. This bends the light beam 90°. The flat mirror does block some of the light from getting to the big mirror, but a lot less than your head would! The big mirror is called the primary, because the light hits it first; the smaller mirror is called the secondary. A telescope with this configuration is called a Newtonian. This design is popular for small, amateur telescopes, because the flat secondary is cheap, and — for an amateur-size, portable telescope — puts the eyepiece at a convenient height off the ground.
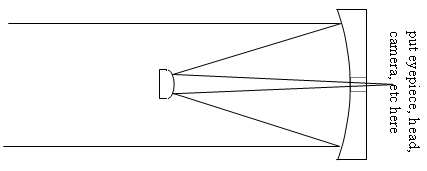
Another solution to the head-in-the-way problem is to place a curved secondary mirror in the light beam, to send the rays back towards the primary mirror and through a hole in the middle of the primary. This design is typical of large research telescopes because it places the instruments (usually CCD cameras or spectrographs) at the bottom of the telescope instead of the top, which could be 100 feet up in the air. This design is called a Cassegrain, after the French scientist Nicolas Cassegrain, who invented it in 1672.
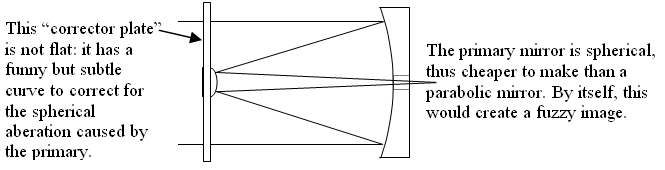
The last kind of reflector I want to tell you about is called a Schmidt-Cassegrain. Newtonian and regular Cassegrains use a parabolic mirror, i.e. they have the shape of a shallow parabola, rotated around its axis. That’s the shape that is needed to make a sharp image of objects at infinity. However, making parabolic mirrors is hard, and therefore expensive. Mirrors are shaped by grinding two pieces of glass together. One of the pieces will become concave and the other convex, and they naturally form a spherical shape — in other words, the curvature is the same everywhere on the surfaces. So making spherical mirrors is easy and cheap. In 1930, Bernard Schmidt invented a way to use a spherical mirror for a telescope primary, by placing a so-called corrector plate at the front of the telescope, near the secondary mirror. This corrector plate is glass, a very thin lens that has a subtle and varying curvature that corrects for the primary mirror having the “wrong” shape. Besides economy, this also produces a telescope with a somewhat wider field-of-view than a standard Cassegrain.
2. Steward Observatory, the Astronomy Department of the University of Arizona, has a facility where they manufacture the world's largest single-piece telescope mirrors --- up to 8.4 m in diameter. They have a unique approach to casting the glass: a oven melts the glass, and then the entire oven is spun on a turntable. The molten glass flows tangentially outwards from the center, forming a parabolic curved shae, just what is needed for a telescope. The oven temperature is lowered, freezing the glass in that shape. They still do fine grinding a polishing of the glass surface, but at least the glass is close to its required shape when it comes out of the oven. Here are a few videos about the process...
Why Do We Build Telescopes?
Having talked about how to build a telescope, let's address why we would want to. What benefits do telescopes provide? There are three things telescopes improve:
- Magnification: making the object appear larger, as if it is closer than it really is
- Collect more light: the pupil of a human eye is rather small. If you have a bigger "bucket" to collect light, you can see things that are fainter and farther away.
- Better angular resolution: see sharper detail.
When we say magnification in this context, we actually mean angular magnification The angular magnification describes how much larger the image looks viewed through the eyepiece, compared to looking directly at the object without the telescope. In other words, it’s the ratio of apparent angular size (seen using the telescope) to actual angular size (seen without the telescope). The magnification can be calculated from this equation:
For refractors, ftelescope is just the focal length of the objective lens. For Newtonian reflectors, ftelescope is the focal length of the primary mirror; for Cassegrains and Schmidt-Cassegrains, ftelescope is complicated because it depends on the curvature of both the primary and secondary mirrors. Most small telescopes have their focal length printed on them somewhere.
Where did the angular magnification equation come from? Watct this video...
Telescopes also collect a lot more light than the human eye, allowing us to see fainter objects. Since one reason an object might be faint is because it's far away, bigger telescopes allow us to see greater distances. And because light takes time to travel — light is very fast, but space is very, very big — the farther away we can see, the further back in time we can observe. With the largest research telescopes we currently have, about 10 meters in diameter, we can see galaxies about 10 billion lightyears away, therefore we are seeing them now as they were 10 billion years ago, when the universe was only about a third of its current age.
EXAMPLE The small refracting telescope we have in class has a focal length of 700 mm. If you put in an eyepiece with focal length of 20 mm, what is the magnification?
SOLUTION
Most telescopes are circular in cross-section, so the light-gathering area of the telescope is just...
If you are comparing the light-gathering areas of two telescopes, then usually we take the ratio of the areas, which equals the ratio of diameters squared.
EXAMPLE How much more light does the Keck 10-meter-diameter telescope collect than a human eye. Assume a typical pupil diameter of 5 mm.
SOLUTION
So the Keck telescope collects roughly 4,000,000 times more light than your eye! All other things being equal, it can see objects 4,000,000 times fainter than your eye. That sounds impressive, but it's even better than that.
- Electronic image sensors used in professional astronomical research cameras (called CCD chips) are about 90% efficient; your eye is about 5% efficient. That is, CCDs are about 18 times more sensitive than your eye.
- Your eye cannot store or record the light. In other words, your eye can’t do a time exposure. The human eye is like a video camera that can’t record, taking “exposures” about 1/10th of a second long. (That’s why you don’t notice the flickering of a movie screen, which shows 24 frames per second.) So, if a CCD camera takes a 1-hour time exposure (3600 seconds), that’s about 36,000 times more than one “frame” of human vision.
So really, a 1-hour time exposure taken with the Keck telescope can see things that are 4,000,000 times 18 times 36,000 times fainter than the human eye. That’s about 3 trillion times fainter!
3. Here is a Powerpoint presentation about telescopes. And some of the embedded movies:
ADDITIONAL ACTIVITIES & PRACTICE
5. An international consortium is hoping to build a 30-meter-diameter telescope on Mauna Kea, Hawaii in the next decade. It's called the TMT, for "thirty-meter telescope". (a) How many times more light will it collect than the Keck telescopes, which are 10 meters in diameter? (b) How much more light will the TMT collect than your eye? Assume your pupil's diameter is 5 mm.
6. My 7-inch Meade telescope has a focal length of 2670 mm, and I have a selection of eyepieces, with focal lengths of 10 mm, 17 mm and 26 mm. (a) Which eyepiece will give the lowest magnification? What would that magnification be? (b) Which eyepiece gives the highest magnification? What is this highest magnification? (c) How much more light does this telescope collect than your eye. (Assume a pupil diameter of 5 mm.)