Refraction

Introduction Light slows down when it enters a transparent medium (like glass) from a vacuum. This causes the direction of a light ray to change when it goes from one medium to another with a different index of refraction, n. The velocity of light in the medium is

, where c is the speed of light in a vacuum, about 3.0x10⁸ m/sec, or 186,000 miles per second.

You've probably seen the symbol c before — usually people call it simply the “speed of light.” Really it's the speed of light in a vacuum; when light is in water or glass it moves slower. Keep that in mind because none of the following will make sense if you don't.

The diagram below shows a ray going from air (n=1.00) to water (n=1.33). The angle of the incoming ray is called the angle of incidence, θi. The angle after the ray goes through the boundary is called the angle of transmission, θt. We measure angles relative to the normal, a line perpendicular to the surface where the ray hits. I've also drawn several wavefronts (crests) on the incident ray: remember that wavefronts are always perpendicular to the rays. Which part of the wavefronts will hit the water first? The bottom edge. The bottom of each wavefront hits the water first and will slow down. The top part is still in the air, going 3x108 m/sec. So the whole ray will bend to be more in line with the normal. This only happens if the ray is going into a medium with a higher n.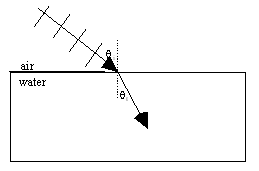

Now, draw another ray coming up from the glass into the air, with some wavefronts. Can you see that that ray, moving into the air from the glass, will bend away from the normal?

Here are the two general rules:

• Rays going into a slower medium bend towards the normal, θ_t< θ_i.
• Rays going into a faster medium bends away from the normal: θ_t> θ_i.

Note that I haven't told you how to calculate exactly what the transmitted angle is in any given situation. We're skipping that.

A light ray going passing through a piece of plate glass will bend towards the normal when it enters, but away from the normal when it leaves. The ray leaving the glass will be parallel to the ray entering the glass, just shifted to the side a little bit.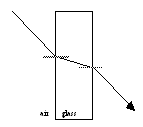
A light ray entering a triangular prism (from air) will bend towards the normal when it enters, but away from the normal when it leaves. (This much is the same, no matter what the shape of the glass.) BUT, because the sides of the glass are not parallel with each other, the ray won't end up parallel to its original direction. The ray in the diagram has been bent downwards at both surfaces of the glass. THINK IT THROUGH!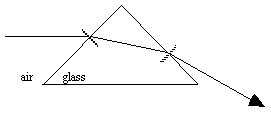
Now, let's take five pieces of glass — one piece of plate glass, two prisms, and two trapezoids — and stack them as shown in the diagram. A ray going through the plate glass doesn't bend; a ray going through the prism bends a lot; the ray going through the trapezoid bends a medium amount. (The prism and trapezoid on the bottom are upside-down, so they bend the rays upward.) If the shapes are right you can make five rays all come to a single point. What we have made is a crude converging lens.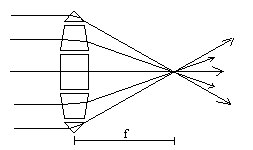

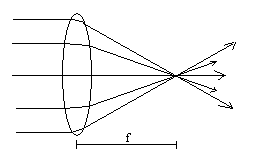
It is better if, instead of separate pieces of glass with straight sides, we use a single piece of glass with smoothly curved sides. The shape is convex. Just like for mirrors, the distance between the center of the lens and where initially-parallel rays converge is called the focal length, f. Because parallel rays come from objects that are at infinity, the image of a very distant object is at a distance f from the center of the lens. Recall that the image of an object formed by converging rays is called a real image.

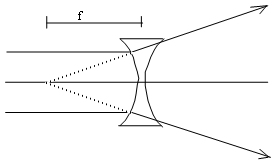
If we make the glass thick at the edges and thin in the middle, the lens shape is called concave and will cause parallel light rays to diverge (spread apart). To someone standing to the right of the lens (as drawn here), looking into the lens, it will look like the rays came from a point to the left of the lens, from where the dotted lines meet. The focal length is the distance between the center of the lens and the point those rays appear to be coming from. To signify that this is a diverging lens (and not a converging lens) we give the focal length a minus sign: it's negative. Recall from our discussion of mirrors that the image formed by diverging rays is a virtual image.

 

Here's a photo of a convex and concave lens, side by side on a windowsill. (Click on it to see a larger version.) The convex lens is the one on the left. Both are creating images of the cars outside: the convex lens is creating a real image that is closer to the camera than the lens itself; the concave lens is creating a virtual image that is further away than the lens (just a few centimeters outside the window.) The camera taking the photo could not focus on both images at the same time because they were at such different distances. I focused the camera on the virtual image, and so the real image is blurry.

Activities & Practice
to do as you read

1. Here's an animation showing wavefronts of light in air entering some transparent material where its speed is cut in half. These wavefronts are moving straight into the slow medium, so they don't change direction. However, if the wavefronts hit at an angle, they will turn, as seen in this second animation.

2. Three brothers went out west to establish a cattle ranch. They could not think of an appropriate name for the ranch. They called their physicist mother back east and she suggested the name "Focus". They were puzzled. "Because that's where the sun's rays meet."
(from Asaac Isimov, Treasury of Humor)

Lenses and Mirrors Compared   To review, the terms convex and concave refer to the shape of a lens or mirror; convex means "bowed outward in the middle"; "concave" means curved inward. The words converging and diverging are describing what those lenses and mirrors do to the light rays that hit them. Converging lenses and mirrors try to make rays come together; diverging lenses or mirrors spread them apart. A real image is created by light rays that actually converge (come together). Such an image can be projected onto a screen or a piece of photographic film or an electronic CCD chip and recorded. Diverging light rays form a virtual image: they merely appear to have come from a particular place.

Concave mirrors and convex lenses do the same thing, namely try to converge light, to create real images.

Concave lenses and convex mirrors do the same thing, namely diverge light to create virtual images.

 

Fresnel Lenses   Keep in mind that the light-bending accomplished by lenses takes place only at the surface, when the rays enter and leave the glass. The angle of the glass surface determines how much each ray bends. The interior of the lens doesn't really serve a function. We could, therefore, get rid of the bulk interior of the glass, and just have the surface curvature of the glass preserved in small segments. The diagram below illustrates the idea. called a Fresnel lens.

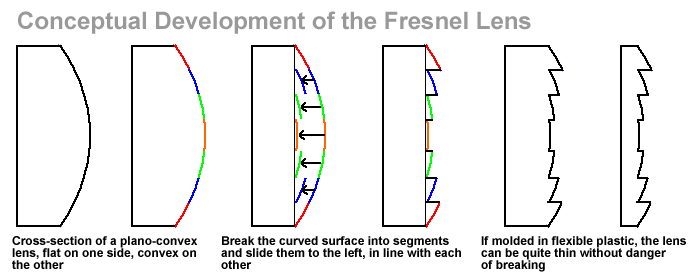
The images below show a fresnel lens, scavenged from an old overhead projector. The left photo shows the entire lens. You can see the (real) upside-down image of the distant cars. The right photo is a close-up, with the camera focused on the lens, rather than the image of the cars. You can see the ridges that do the focusing — near the center the ridges are nearly flat; further from the center they are increasingly steep. Click either image to see a larger version.

Birefringence (Double Refraction) Some transparent crystals have differing indices of refraction depending on the polarization of the light passing through them. Calcite is a good example. Light passing through calcite, containing a mixture of polarization components in perpendicular directions (relative to axes defined by the crystal structure), will be bent in two different directions. Here's a short video showing a calcite crystal doing its thing.

Additional Activities and Problems

4. Watch the video below. Explain why you can see the coin at the end. Include a diagram as part of your explanation.