Reflection

Introduction   

When we are talking about reflection, we are usually talking about specular reflection. This is reflection from smooth, shiny surfaces like mirrors. (Speculum is the Latin word for 'mirror'.) Let's say we have a mirror, and a light ray that is hitting it. How can we predict where the ray will go? We use the Law of Reflection: the angle of incidence equals the angle of reflection. We'll use the symbols θi and θr to represent these angles. Both of these angles are traditionally measured from the normal — a line that is perpendicular to the surface of the mirror. Written as an equation then, the law of reflection is

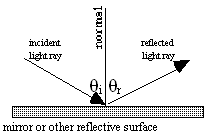This law not only helps you follow where a light ray goes after hitting a mirror, but also is handy when playing billiards.

Diffuse reflection is the more common kind of reflection. It's what allows us to see each other and other objects in our environment. Light from the sun or some other source hits an object and scatters in all directions. So anyone standing near that object will have some light rays that bounce off the object enter their eyes. The reason this happens is that the surface is, on the microscopic level, very rough. The light is reflecting off of many "mirrors" at all different orientations. At each microscopic spot where light hits the surface it obeys the law of reflection, but because the surface is rough, light rays end up going in all different directions.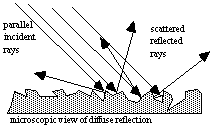

Here are a few photos from NASA showing reflections in the solar system:

	The Pacific Ocean, as seen from the International Space Station. The Sun is just out of the frame, top center, but you can see sunlight reflected in the ocean below. (You can also see towering thunderclouds and their shadows.)
	Saturn's largest moon, Titan, as seen in 2009 by the Cassini spacecraft. You're seeing mostly the nighttime side of Titan, with a thin crescent of the daytime side visible. The glint at the top is specular reflection of sunlight (the Sun is out of the frame, above the middle top of the picture) off a lake near the north pole. Titan is the first planet or moon discovered to have liquid on its surface, other than Earth, of course. The liquid on Titan is not water (it's far too cold for water to be liquid) but is likely to be liquid methane and ethane.
	This is a radar image of part of Titan, near its north pole. The black splotches are lakes. The reason they are dark is because the Cassini spacecraft sent out (transmitted) radio waves, which then reflected off the surface. The surfaces of the lakes are smooth like a mirror, and the reflections are specular. Since the radar transmitter was not aimed straight in (normal) to the lake surfaces, the radio waves reflected off in some direction according to the law of reflection, but NOT back to Cassini. The surrounding land surfaces are rough, so the radio waves reflect off them diffusely. Some of the radio waves end up going back to the Cassini receiver.

Now that we've discussed the difference between specular and diffuse reflection, everything we'll discuss from now on will be about specular reflection.

When you look at yourself in the bathroom mirror, light from the room is bouncing off of you, reflecting off the mirror, and entering the pupil of your eye. The diagram here shows a single ray coming from your foot.

When that ray enters your eye, your brain assumes it came in a straight line. So the "mind's eye" constructs a picture of an identical person standing an equal distance behind the mirror. This is a virtual image. (Virtual means 'unreal'. The image is described this way because the light rays never actually reach the place where the image is. In this case, the image is behind the mirror, but the light rays never go through the mirror.)

This video will explain in greater detail. Click to watch it.

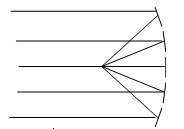
A concave mirror can create a real image, as opposed to virtual. Imagine having five flat mirrors placed like in the diagram below. By aiming the mirrors correctly, you can make the five parallel rays all reflect towards the same point.

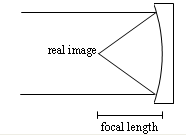
Now, instead of actually using many small mirrors, just make one mirror with a curved, concave surface, like in the diagram below. This is a converging mirror because it causes parallel light rays to come together (converge).

The distance between the mirror and where parallel rays come to a focus is called the focal length, f. You can put a projection screen or a piece of photographic film where the rays converge and get a picture of whatever distant object the mirror is pointing towards. This is a real image (the rays actually reach the spot where the image is.) This is different from a virtual image, because you aren't looking 'through' the mirror in order to see the image.

For a given mirror, the focal length is a constant, determined by the curvature of the glass.

Activities & Practice
to do as you read

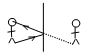
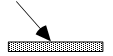
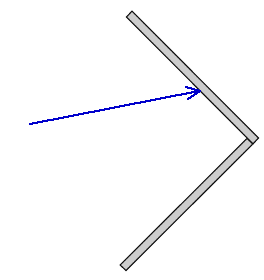
1. Draw the normal and the reflected ray from this mirror. Use a protractor to be precise.

2. What must be the direction of the incident ray in order for it to return exactly to where it came from, after reflecting off a flat mirror?

3. Go to your bathroom mirror and look at yourself. Hold up your left hand. What hand is the reflection holding up?

4. You have two flat mirrors oriented at 90° to each other, as shown in the diagrams below. Three light rays come from the left and hit one of the mirrors, at three different angles. Draw carefully (with a ruler and protractor) the path the light ray takes in each of these cases. What do you notice about the final reflected ray (after it reflects from the second mirror) in each of the three cases?

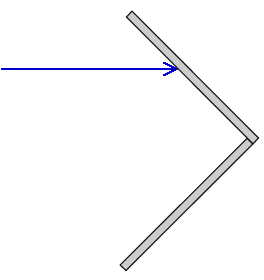
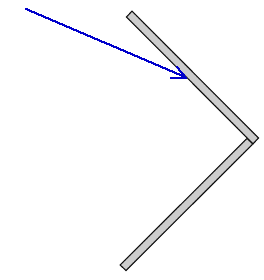
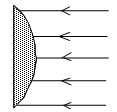
5. Which of these three curved mirrors do you think has the shortest focal length?

6. Draw what happens to the rays that hit this convex mirror.

Additional Activities & Practice

7. How many curved mirrors do you encounter in your life? List as many as you can.

Follow-up to Problem 4: Three of the six successful Apollo landings on the Moon carried retroreflector panels. The astronauts left them on the surface, some distance away from the Lunar Module (LM) so they wouldn't be damaged or covered by dust blown by the LM's liftoff. The first two photos below show the panel deployed during the Apollo 11 mission. The third photo shows a laser beam being fired at these retroreflectors from the McDonald Observatory in Texas. By measuring (very accurately!) the time needed for the light to reflect back, the distance to the retroreflectors can be calculated to a precision of a few millimeters! Two robotic rovers landed on the Moon by the Soviet Union also carried retroreflector panels.

This all seems very exotic, but closer to home retroreflectors are also molded in plastic to make safety "reflectors" for bikes, cars, running shoes, telephone poles, etc. Anything you wouldn't want cars crashing into at night. Here are a few pictures of one. The first two photos are the front and back sides of the reflector, respectively, magnified 10 times. In the second you can see the three-sided-pyramid shape, each one like the corner of a cube that's been chopped off. Like in problem 4, the reflecting faces of a cube are all perpendicular to each other, so this shape will return a light ray backwards, exactly in the direction it came from. In fact, retroreflectors are also often called corner-cube reflectors. The last picture is zoomed in even closer, 60x magnification.

Retroreflectors are also on the tops of the staffs used by modern surveying crews. The surveying instrument, a "theodolite", measures the direction to the staff, and also shoots a laser at the retroreflector to determine the distance.