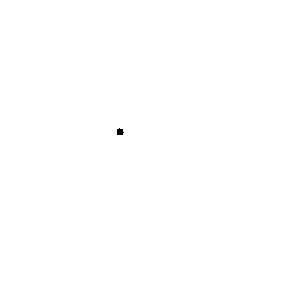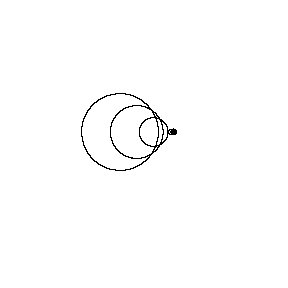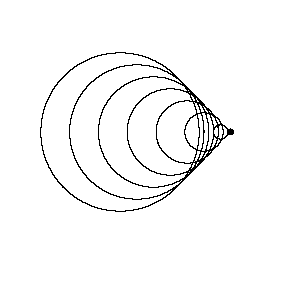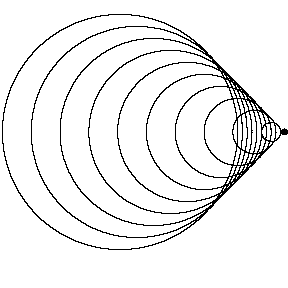Doppler Effect & Shocks

Introduction Listen to this sound clip. It's a car driving past with its horn blaring. Notice two things: first, the horn gets louder as the car gets nearer, then quieter after the car has passed and is now receding. Secondly, notice that at the moment the car passes the pitch (frequency) of the sound suddenly drops. That change in frequency is due to the Doppler Effect. We'll use some diagrams to explain why this happens.

First, imagine a car that is standing still, with its horn sounding. Below is a diagram showing this situation from above. The concentric circles represent the wavefronts (compressions) of sounds waves, moving outwards away from the car at the speed of sound. The distance from one compression to the next compression is the wavelength.

Now imagine the car drives off, still with the horn blaring. The compressions are closer to each other in the direction of the car's motion. In other words, the wavelength is less. On the opposite side, the compressions are relatively far apart — longer wavelength. Why does that happen? Each wavefront is a circle, expanding outwards from where it was created. Each expanding circle remains centered on the spot where it was created, but each successive wavefront is centered on a different spot because the car is moving. Anyone standing in front of the car will hear a shorter wavelength, which means a higher frequency. Behind the car, a listener will hear a higher wavelength (low frequency).

Although our imaginary example here was a car emitting sound waves, the Doppler Effect happens with all waves: light, water waves, as well as sound.

Regardless of which is moving, the source or the observer, the greater the velocity, the greater the change in frequency (or wavelength) compared to when the velocity is zero. It is this fact that makes the Doppler Effect a useful tool for measuring velocities.

Activities & Practice
to do as you read

Play with this wave Doppler simulation by David Harrison at the University of Toronto.

Examples of the Doppler Effect. Here are some examples from everyday life, as well as more esoteric but cool applications.

As in the audio clip above, you can hear the sudden frequency shift of race cars, ambulance sirens and car horns as the vehicles pass you.
Police "speed gun" radars sends out radio waves that bounce off cars. The reflected radio wave has its frequency shifted: the faster the car is moving, the more the frequency is changed. The radio receiver measures the changed frequency, calculates the car's velocity and displays the result. Baseball speed guns work similarly. They can only measure the velocity towards or away from the radar gun, but not an velocity component in the perpendicular direction.

Click to enlarge.

Traditional radar used for tracking airplanes and thunderstorms sends out radio waves and times how long it takes for the reflection to return. The radar system can then calculate and plot the location of reflecting airplane or thunderstorm. Velocity is determined by calculating distance/time. Newer, Doppler radar systems can do all that, but also measure the change in frequency of the reflected radio waves, thus allowing the velocity to be calculated faster and more accurately.

Click to enlarge.

Astronomers can measure the frequency (or wavelength) change in light and radio waves coming from celestial objects, and can thus measure their speed towards or away from Earth. Of course, the Earth is moving too, but the effect of the Earth's motion can be subtracted from the calculation. Using the Doppler shift, astronomers have...

determined that the Universe is expanding. The galaxies are moving away from each other, and the speed is greater the farther away the galaxies are. This is was first discovered in the 1920s by Edwin Hubble and was our first solid evidence that the Universe had a beginning, what is now usually called the Big Bang.
determined that the Milky Way galaxy is a spiral galaxy, similar to M31 (the Andromeda Galaxy, photo below.) The Sun is one of about 300 billion stars in the Milky Way, but because we are located inside it, and visible light is blocked by lots of obscuring dust floating between the stars, it is hard to get a good view of its structure. Radio waves emited by neutral hydrogen gas, however, penetrates through the dust. By measuring the Doppler Effect of those radio waves, the gas's velcity can be calculated. Do that for gas in different directions in the sky and the spiral structure of our Galaxy can be detected.
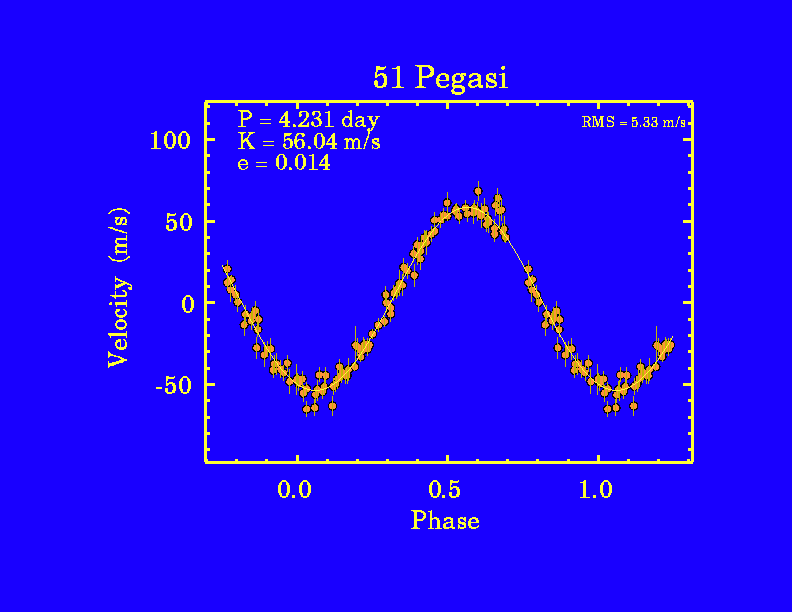
since 1995, discovered about 800 planets (as of 2012) orbiting stars other than the Sun. We have no pictures of these planets yet. The gravity of a planet causes its parent star to move, to orbit around the star-planet center of gravity. The motion of the star can be detected using the Doppler Effect on its light, and the existence of the planet discovered. The orbital period and lower limit of the planet mass can also be calculated.

Click to enlarge.

Here's an animation illustrating the Doppler Effect in measuring the motion of the two stars of a binary star system.

I have a great song about the Doppler Effect. Remind me in class to play it for you.

The Math of the Doppler Effect

For waves, the Doppler Effect can result from motion of the source of the waves, the "observer" (a microphone or ear, if we're talking about sound), or both. This video (click below) derives the equation.

The punchline of the video is that

EXAMPLE: A flat-bed train car has a piano sitting on it. The pianist, despite being a great piano player, is only hitting the A4 key, 440. Hz, over and over again. The train is traveling at 60.0 km/hr coming towards you, standing by the side of the tracks. What frequency do you hear? PLAY VIDEO

EXAMPLE: A flat-bed train car has a piano sitting on it. The pianist is only hitting the A4 key, 440 Hz, over and over again. How fast does the train car have to be moving towards you, standing by the side of the tracks, so that you hearnot an A note, but rather a B, 494 Hz? PLAY VIDEO

EXAMPLE: Bats use ultrasound echolocation to detect both the distance and the velocity of prey. Let's say a bat sends out an ultrasound pulse with frequency 76.5 kHz, and that sound bounces off a moth that is 7.0 meters away moving at a speed of 2.0 m/sec directly away from the bat. What is the time delay of the echo, and what is the frequency of the echo the bat hears (which is shifted because of the Doppler effect)? PLAY VIDEO

When talking about the Doppler Effect with light, the velocity of the observer and the source are almost always going to be miniscule, compared to the speed of light. In this case, the equation simplifies dramatically. Expressing the Doppler Effect in terms of the change of wavelength instead of the observed frequency, the result is that

Shocks Something interesting happens when the velocity of the source equals or exceeds the wave speed. The crests of the waves pile up, forming a very strong area of constructive interference called a shock. If the waves are water waves (for instance, caused by a moving boat on a lake), the shock is called a wake. If the waves involved are sound waves, the shock is called a sonic boom. Here's an animation showing the waves when the source speed equals the wave speed.

Here's how it looks when the source velocity is greater than the wave speed.

Below are two photos showing the shocks from objects moving at supersonic (faster-than-sound) speeds. The first shows a rifle bullet; the other is a T38 jet aircraft, traveling at Mach 1.1.

Click to enlarge.

Here are two sound files illustrating how sonic booms can sound: 1 2

Other photos of shocks. Click a photo to see an enlargement.

	A duck or a boat that moves faster than the speed of water waves creates a shock. Notice how the v-shaped wake looks like the sonic boom pictures above.
	A schlieren image of a balloon just a moment after it has burst.
	Schlieren images of various shapes inside a supersonic wind tunnel. These images were taken to study possible shapes of capsules for the Mercury space program. You might think a pointy object would be best for "cutting through the air", but there's a problem: pointy objects come into contact with the shock (like in the top-left picture), which is hot, causing damage to the object. If the object is blunt, however, the shock stands away from the object a little bit, causing less heat to be transferred. That's why the capsules used in the Mercury, Gemini and Apollo programs, and nuclear warheads on ICBMs (intercontinental ballistic missiles) are cone-shaped and re-enter the Earth's atmosphere blunt end first.

	Aerial view of battleship USS Iowa's 16-inch cannons firing. Notice the impact of the shock with the water surface.
	This is a nuclear reactor core, surrounded by water. Nuclear reactors work by splitting Uranium nuclei with neutrons. Each nucleus that splits releases more neutrons, which continue the chain reaction. The released neutrons are initially moving very fast. Faster than the speed of light, actually. Wait, you say? You've heard that it's impossible to go faster than the speed of light? Not true! It's impossible to go faster than c, 3.00x10⁸ m/sec, the speed of light in a vacuum. Light in water, however, moves significantly slower than c, and the neutrons can (and do) exceed that slower speed. When they do, they create Cherenkov radiation, that blue glow. What a sonic boom is for sound, Cherenkov radiation is for light.
	High-power rifle shot. The spherical shock, expanding outward at the speed of sound, is from the exploding gunpowder. You can see the V-shaped shock from the bullet, which is traveling faster than the speed of sound, moving to the left.
	A space shuttle as it is accelerating past the speed of sound.

Additional Activities & Practice

HTML Comment Box is loading comments...