Standing Waves & Resonance
Introduction Recall that interference happens when waves overlap each other. One special case of this occurs when a wave overlaps a wave moving in the opposite direction. Look at the animation below. There are two transverse waves, one (yellow) moving to the right, and another (white) moving to the left. The pink wave is the resulting superposition (i.e. the combination). Examine it carefully.

Credit:
Lee
Amosslee. Click for larger version.
Be sure to notice that:
- The pink wave does not appear to be moving left or right. In other words, it isn't propagating. That's why it's called a standing wave.
- Some spots along the standing wave are not moving at all — the amplitude is zero. These are called nodes. There are 6 nodes in this animation, including at the extreme left and right. Other locations, halfway between the nodes, have big amplitude. These are antinodes. There are 5 of them in the animation.
- The distance from node to node (or antinode to antinode) is half the wavelength. Remember this, because it is key to understanding
Why do we care about standing waves? Because virtually every musical instrument creates sound through standing waves. Violins, guitars and pianos use strings: vibrations created when a string is bowed, plucked or hit reflect back-and-forth along the string, creating standing waves. In flutes, organs and marimbas, sound waves travel back-and-forth inside tubes.
to do as you read
Resonance One situation in which standing waves occurs is when a wave encounters its own reflection.
Go back to the simulation at http://phet.colorado.edu/simulations/stringwave/stringWave.swf. Turn on the 'oscillate' option, set the amplitude, frequency and damping to 5, 50 and 0, respectively. Hit 'reset' to start the simulation from scratch. Watch what happens over the next minute or two. A standing wave develops, and its amplitude becomes huge even though the amplitude of the oscillation by the little motor is very small. This is because the new waves being produced by the motor interfere constructively with the previous waves that have reflected from the far end of the string. This is called resonance, and it only happens for particular values of the frequency. Reset the frequency to an different value, like 55 (and hit 'reset' again to start over). Notice that the wave amplitude does not increase nearly as much. Again, only particular frequencies experience resonance.
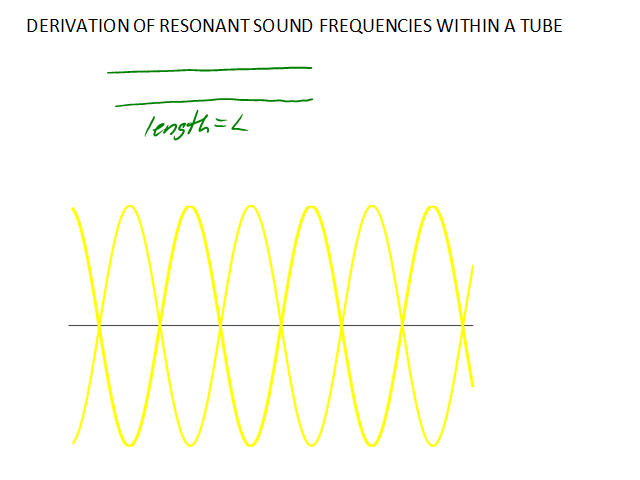
What determines which frequencies resonate in, for example, the tube of a flute? Only certain wavelengths satisfy the boundary conditions, mathematical conditions that must be true at the ends of the tube. This video will show how these boundary conditions are used to derive the equations for the resonant frequencies.
To summarize, if there are nodes at both ends, or antinodes at both ends, then the frequencies produced are fo, 2fo, 3fo, 4fo, etc., integer multiples of the fundamental frequency, fo.
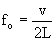
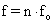
The other frequencies, multiples of the fundamental, are called harmonics.
These equations apply to flutes, piccolos, and organ pipes, all of which are open at both ends, so both ends are antinodes. In wind instuments such as these, v (the velocity of the wave) is just the speed of sound. These equations also apply to violins, guitars, and pianos, where both ends of each string are clamped down, forcing them to be nodes. However, in stringed instruments v is not the speed of sound. Instead, it's the speed of the wave traveling along the string, and that depends on the density and thickness of the string, and the tension it is under. Denser and thicker strings have lower frequencies (more inertia means they don't wiggle as fast). The tighter the string is pulled, the higher v is and the higher frequencies are created.
If there is a node at one end and antinode at the other, then the frequencies are fo, 3fo, 5fo, 7fo, etc., the odd multiples of fo. The fundamental frequency in this case is half what it was above, namely,
1. Find the fundamental frequency for a flute-like instrument, open at both ends, that is 1 meter long. What are the values of the first three harmonic frequencies?
2. Find the fundamental frequency for a tube, open at one end and closed at the other, that is 1 meter long. What are the values of the first three harmonic frequencies?
3. How long is a tube, closed at one end, that has the same fundamental frequency as the open-ended tube in problem 1?
4. How long does a tube have to be to produce a 512-Hz fundamental if (a) it's open at both ends, and (b) it's closed at one end, open at the other.
5. Have you ever been in a car at a stoplight listening to the radio? Sometimes the reception is real bad, but if the driver lets the car creep forward a few inches, the radio reception will be fine. This happens because there is destructive interference between two waves at the location of the car's antenna: the radio wave coming straight from station's transmitter, and a reflection of that wave, coming from some nearby building. If the two waves are out of phase, then reception of the signal will be poor. Assuming the radio station's transmitter, your car, and the reflecting building are all in a line, how far must you move the car (in terms of the wavelength) to change the destructive interference to constructive interference?
6. Have you ever listened to the sound created when you fill a bottle with water? Not just heard, but listened? Play this video, and the sound will surely be familiar. Explain why the sound frequency rises as it does.
Other examples of standing waves
- Theatre and Concert hall dead spots
- Uneven cooking inside a microwave oven
Additional Activities & Practice
7. SPREADSHEET: Create a spreadsheet with one input cell, the length of a tube. Then make two calculated columns, with the fundamental and first three harmonics for (a) a tube open at both ends, and (b) open at one end.
8. The Rubens' Flame Tube: watch this video. Can you determine the speed of sound in the propane gas?
9. The whistles used by police officers in London (“bobbies”) actually have two whistles inside. One produces a tone of 2136 Hz, and the other a tone of 1904 Hz. When blown, it sounds like there are three tones: 2136 Hz, 1904 Hz, and the beat tone.
|