Converting Vectors between Magnitude-Direction and Component descriptions
Finding components from the magnitude and direction. Let's say you
have a vector. Call it 
. If
you know the magnitude (A) and direction θ of
this vector and need to know its components, then use
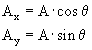
The direction θ is measured counterclockwise from the positive x-axis.
to do as you read
Finding magnitude and direction from the components. Conversely, if you know the components of a vector, and need to know its magnitude and direction, then use
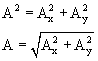
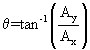
Beware the inverse tangent (arctangent) function. It cannot distinguish between directions in the I and III quadrants, and also cannot distinquish directions in the II and IV quadrants. Most calculators and computer arctangent functions will give you the direction in the I and IV quadrants. If you know the direction is actually in the II or III quadrants, just figure out what the exact opposite direction is by adding or subtracting 180°.
Additional Activities & Practice
1. Josephine is pushing a box across the floor, by pushing with 65 pounds of force at an angle of 25 degrees below the horizontal.
(a) Carefully draw this vector to scale, then draw the horizontal and vertical components of the force. Based purely on this drawing (i.e. not using trig) determine the magnitudes of the x- and y-components.
(b) Now calculate the x- and y-components using trig.
2. A train is traveling at 12.00 m/sec. Inside, the conductor tosses a ball straight upwards at a speed of 3.00 m/sec. According to someone standing on the ground outside the train, how fast and in what direction is the ball moving when it leaves the conductor's hand.
3. Clyde has a canoe and wants to cross a river. The river is flowing at 4.0 m/sec. Clyde aims the canoe straight across the river and paddles at a speed of 2.0 m/sec relative to the river, but because the river is flowing, he doesn't go straight across. In what direction does he move, and how fast?
4. An airplane is flying in the direction 35 degrees North of West at 450 miles per hour. Calculate the westward and northward components of the velocity.