Vectors
   
Introduction  A vector is any physical quantity that has both a magnitude and a direction. (Something that does not have a direction, such as mass or temperature, is called a scalar.)

Some examples of vectors are:
• position: a distance and direction relative to the origin of some coordinate system
• displacement: a change in position
• velocity: a speed in a particular direction
• force: a push or pull

We’ll be using variables to represent vectors, but it’s helpful to have some way of distinguishing a vector variable from a scalar. We’ll do that by putting an arrow over the vector’s variable, like this...

The magnitude of a vector is symbolized by the letter without the arrow, or by using double bars (similar to the absolute-value symbol).
                            

Like absolute value, the magnitude of a vector is always positive.

 

 Activities & Practice
to do as you read

Measuring Directions  Directions can be measured in several ways.

  • Geographic system  In problems involving horizontal vectors on the Earth, it’s often convenient to use north, east, south and west (the cardinal directions) as reference directions. (Usually, North is up on the map page, East to the right, South is down, and West is left. Mnemonic: "Never Eat Soggy Waffles!") For example, the direction "10° East of South" means the direction is close to South, but rotated 10° towards the East. That is direction A on the diagram below. As another example, the direction "25° North of West" (direction B) is close to pointing West, but rotated 25° toward the North. Note that this is not the same as "25° West of North", which is closer to North, but rotated 25° towards the West (direction C). Direction C can also be described as "65° North of West." Using this system, the number is always between 0° and 90°.

                                 

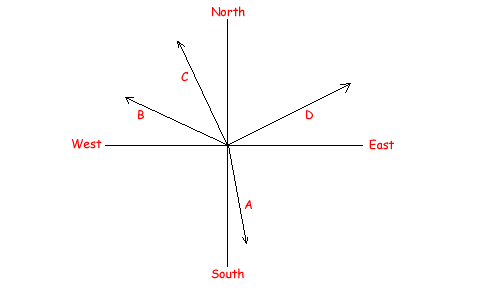
  • Azimuth system  There's another, simpler, way to indicate direction. The azimuth system defines North as 0°, East as 90°, South as 180°, and West 270°. In other words, we measure the direction clockwise from North, from 0° to 360°. This is the system used in compasses, so you might hear this referred to as "compass direction." In the above diagram, A is azimuth 170°, B is 295°, and C is 335°.
  • Mathematical system  In other problems with two perpendicular axes (usually, x and y), it is traditional to measure angles counterclockwise from the positive x-axis, pointing to the right (East in the above diagram.) Again using the above diagram as an example, direction A is 280°, direction B is 155°, and direction C is 115°.
  • Ad-hoc systems: “Ad-hoc” means “made up on the spot; improvised”. You might run into problems like "a circus performer is shot out of a cannon that is tilted 40° above the horizontal..." or "a car collides with a wall at a 35° angle with the wall..." These pieces of information only make sense within the context of a particular problem.

 

1. Measure the direction of vector D in the diagram to the left. Give the direction in the geographic system, the azimuth system, and the mathematical system.

 
Setting a scale  When drawing vectors, we'll need to set a scale, a way of relating the real magnitude of the vector to its length drawn on the paper. For example, a displacement vector of 30 km could not be drawn full-size on your paper! Instead, you could decide that each cm on the paper would represent 5 km in the real world. That would make a 30 km vector 6 cm long on your drawing. Be sure to label your drawing with the scale you used.

2. Draw a set of geographic axes, set a scale, and draw the following vectors. (Don't forget to write down the scale you used.)

A: 20m, 35° S of W
B: 35m, 190° azimuth
C: 18m, 35° W of S
D: 11m, 22° (mathematical)

 

  

 

HTML Comment Box is loading comments...