Vector Components
DEFINITION: Given a vector ![]() ,
the components of
,
the components of ![]() are
2 other vectors
Ax and Ay, parallel to the x- and y-axes, respectively,
whose vector sum is
are
2 other vectors
Ax and Ay, parallel to the x- and y-axes, respectively,
whose vector sum is![]() .
The process of finding the components of a vector is called resolution.
.
The process of finding the components of a vector is called resolution.
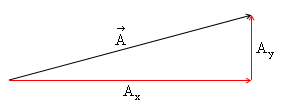
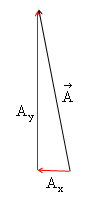
You can think of resolution as kind of like the opposite of vector addition. Adding two vectors together, you draw them head-to-tail, and find the resultant. On the other hand, to "resolve" a vector, you ask what two vectors, added together (head-to-tail) give you the vector. There are an infinite number of pairs of vectors that sum to any given vector, but there is only one pair that are parallel to the coordinate axes. These are the components.
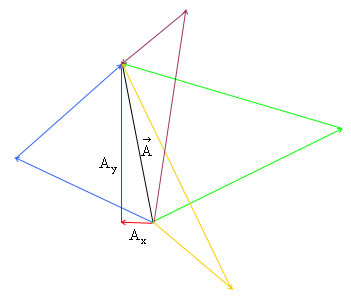
The diagram below shows the vector![]() from
the right-hand diagram above. The yellow, green, blue and purple pairs
of vectors all sum to the vector
from
the right-hand diagram above. The yellow, green, blue and purple pairs
of vectors all sum to the vector![]() ,
but only the red vectors are the components of
,
but only the red vectors are the components of![]() .
.
Activities & Practice
Print the diagram below. For each of the three vectors, draw the components. Assume these are forces, with a scale of 1mm:30Newtons. In addition to your drawings, tell me what the magnitude of each vector is, and the magnitudes of the components. Lastly, measure the direction of each vector, in the mathematical system.
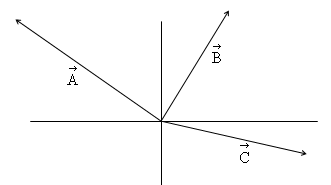
| magnitude | x-component | y-component | direction |
| A= | Ax= | Ay= | |
| B= | Bx= | By= | |
| C= | Cx= | Cy= |