Simple Machines
If you'd like to have this page read to you, click here.
Introduction Let’s say you want to lift a very heavy object. For instance, a 1000-Newton crate carrying a giant watermelon that you need to lift one meter onto a truck to take to the State Fair competition. The problem is, you aren’t strong enough to lift 1000 Newtons. What can be done? Lifting that 1000 N a height of 1 meter will require 1000 J of work to be done, the gravitational potential energy it will gain in being lifted. What if you had a magical device that would let you do that work by exerting 500 N for 2 meters, instead of 1000 N for 1 m? Well, there are several such devices that will do the trick, but they aren’t magical at all. They’re called ramps, levers and pulleys.
BIG IDEA: Simple machines (such as ramps, levers and pulleys) allow you to accomplish a certain amount of work by exerting a smaller force. The trade-off is that you have to exert that force for a greater distance. The work you have to do is not lessened by using the machine. There ain't no such thing as a free lunch.
Activities & Practice
to do as you read
For example, a mechanical advantage of 2 means you only have to exert half as much force (but you’ll have to exert that reduced force for twice the distance).
In the real world, there might be significant friction in your ramp, pulley or lever. The ideal mechanical advantage (IMA) is the mechanical advantage if there is NO friction present. This will equal the ratio of the distance you exert the force with the machine, to the distance you would have to pull without the machine.
Remember: IMA is the ratio of the distances. MA is the ratio of the forces. Only if there's no friction will those two ratios be equal.
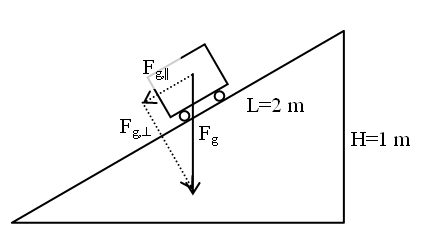
RAMPS In order to push an object up a ramp, you don’t need to push with the full weight of the object. Instead, you only have to push hard enough to overcome the component of weight parallel to the ramp, Fg,||, plus whatever friction there is. Let’s assume the crate has wheels so the amount of friction is negligible. If the ramp is half as high as it is long (along the hypotenuse), then Fg,|| will also be ½ of Fg,. Notice that the force triangle in the diagram below is similar to the ramp triangle (in other words, one is the same as the other, only bigger).
So, in the general case of a ramp of height H and length L, the IMA will be equal to L/H.
1. A ramp is made from a 3.5 meter board leaned against a 1.2-meter high loading dock.
(a) What is the IMA?
(b) How hard do you have to push, in pounds, to get a 500-lb cart up the ramp, assuming no friction in the wheels?
LEVERS A lever is like a playground see-saw, but the pivot usually isn’t in the center. The pivot point of a lever is also called a fulcrum.
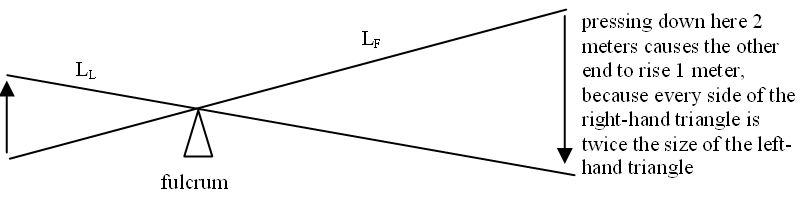
The diagram above shows a lever with mechanical advantage equal to 2. In general, for a lever with length LF on the side where you exert the force, and length LL on the side the load is on, the IMA is equal to LF/LL.
2. A lever is 2 meters long overall, with the pivot located 50 cm from one end.
(a) What is the IMA?
(b) How far will the load move if you push your end of the lever down 40 cm?
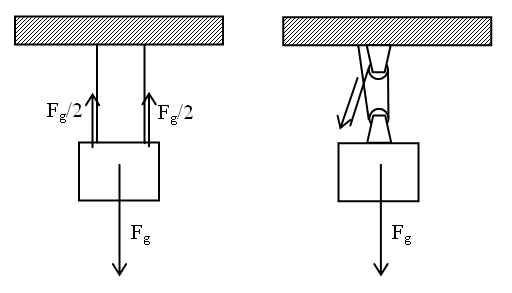
PULLEYS Imagine, for starters, that our 1000-N box is hung from the ceiling with two vertical ropes, like the left-hand diagram below. The tension in each rope will be equal to half the weight. Also, notice that making both ropes 1 meter shorter (in other words, cutting out 2 meters of rope) will lift the load 1 meter higher.
Now imagine a single, long rope is tied to the ceiling, looped around a pulley attached to the weight, and then around another pulley attached to the ceiling, as shown in the right-hand sketch, above. Notice that two segments of rope are supporting the weight, even though it is really one long rope. The tension of the rope is acting on the load twice. The tension is 500 N, and so you only have to pull with that force to hold the weight or raise it with constant speed — the mechanical advantage is 2. (If there is friction in the pulley axles, you’ll have to pull a bit harder than 500 N.) To raise the weight one meter will require pulling 2 meters of rope.
To have different mechanical advantage, you can attach more than one pulley to the ceiling or the object, and loop the rope around more times. Also, the end of the rope can be tied to either the ceiling or the load. The IMA is always equal to the number of rope segments supporting the load.
3. Design a pulley system with an IMA of
(a) 1
(b) 2
(c) 3
(d) 4
Examples
Let's say you need to lift that 1000-Newton crate, to a height of 1 meter,
and you can push or pull with a force of 200N.
(1) How long a board do you need to make a ramp that will do the job. Assume
the crate is on a cart with frictionless wheels.
SOLUTION: You need to reduce the force to 1/5th of the weight of the crate. In other words, you need a MA of 5. Assuming that there's no friction, a board 5 meters long will work.
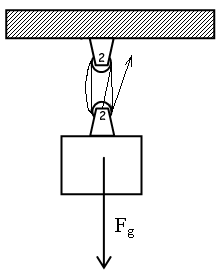
(2) Design a pulley system that will allow you to do the job.
SOLUTION: The pulley system must have an IMA of 5, so 5 rope segments must be supporting the crate. A double pulley on the ceiling, and a double pulley attached to the crate, are indicated on the diagram below with the 2's next to them. One end of the rope is tied to the bracket of the lower pulley; the rope then wraps around one of the upper wheels, around a bottom wheel, around the other upper wheel, around the second lower wheel, and ends up being pulled upwards by you. Assuming there's no friction, you'll have to pull with 200 Newtons of force, and to lift the crate one meter will require you to pull 5 meters of rope.
5. How can you increase the mechanical advantage of a ramp?
6. Specifically, describe a ramp you could use to raise an object while
exerting a force only 1/3 its weight.
7. How can you increase the mechanical advantage of a lever?
8. Specifically, describe a lever you could use to raise an object
while exerting a force only 1/3 its weight.
9. How can you increase the mechanical advantage of a set of pulleys?
10. Specifically, describe a pulley system you could use to raise an
object, exerting a force only 1/3 of its weight.
Efficiency The mechanical efficiency of a simple machine is the ratio the work get out of a machine (the output) to the work you put into it (the input).
For example, if you do 2000J of work, but only get 1500J of work out of the machine, then the efficiency is 75%.
The efficiency is also equal to the ratio of the machine's mechanical advantage to its ideal mechanical advantage.
efficiency = MA/IMA