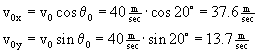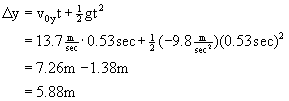Projectile Motion

Basics  A projectile is any object on which the only force acting is gravity and air resistance (drag).

Examples of projectiles are:

• baseballs and softballs in the air after being hit by the bat
• golf balls hit by a club
• objects dropped from aircraft, such as people (skydivers), bombs, crates of food being dropped to refugees
• objects launched by cannons, such as cannonballs, shells, and circus performers

Once the baseball, softball, golf ball, skydiver, bomb, crate, cannonball, shell, or clown are no longer touching the bat, club, aircraft, or cannon, and are in the air with only gravity and slight air resistance acting on it, then it is a projectile.

Here is an online projectile motion applets to play with, just for fun.

• http://galileoandeinstein.physics.virginia.edu/more_stuff/Applets/Projectile/projectile.html

Unless otherwise stated in a particular problem or discussion, we will be ignoring the effects of air resistance.

The key to understanding the motion of projectiles is that the horizontal motion and the vertical motion of the projectile are independent of each other. So we can write separate equations for the displacement of the projectile in the horizontal (x) and vertical (y) directions.

The only common variable between these two equations is t, the time. Because in projectile problems there is usually no acceleration (i.e. we ignore air resistance) in the horizontal direction, we can write

The velocity components follow the same equations we used for one-dimensional motion.

Because there is usually no acceleration in the x direction, the x-velocity is constant.

Here's an Interactive Video Vignette from the fine physics folks at RIT and Davidson College.

Here's a classic projectile motion physics problem, the Monkey and Ranger.

Activities & Practice
to do as you read

Go to this Cannon simulation applet and play with launching projectiles, answering the questions posed below. Vary the launch speed and the projection angle. If available, turn on the "show velocity" option so the simulation will include the horizontal and vertical components of velocity as the cannonball moves. Set the height of the platform to zero meters and answer these questions:

1. Which component of velocity remains constant, and which changes?

2. If you double the launch speed, what happens to the range (x-distance the projectile travels)?

3. If you double the launch speed, what happens to the hang time (the time from launch to landing)? (Note: time is given in the upper right-hand corner of the simulation.)

4. For what launch angle is the range the greatest?

Mathematical projectile problems come in lots of variations. Here are some pointers:

• Draw a sketch, and put a coordinate system on it.
• Write down all the information given in the problem, converting the words into the mathematical variables we use in the equations.
• If you are given the magnitude and direction of the projectile's initial velocity, calculate the horizontal (x) and vertical (y) velocity components.
• Use other information in the problem, and either the horizontal or vertical equation, to calculate the time needed for the flight.
• Use the other equation to calculate the answer to the problem.

Example An archer shoots an arrow horizontally at a speed of 40.0 m/sec, aiming directly at the center of a target 20.0 meters away. How much time will it take the arrow to hit the target? How far below the bullseye will the arrow hit?

The initial velocity is purely horizontal, so we can say that v_ox=40.0 m/sec and v_oy=0 m/sec without doing any calculations.

Also from the problem statement, we can write Δx=20.0 m.

Now, let's start calculating...

Use the horizontal equation to calculate the time needed to hit the target.

       

Now that we know the time, we can plug that into the vertical equation.

       

Example An archer shoots an arrow at an angle of 20.0° above the horizontal at a speed of 40.0 m/sec. The target is 20.0 meters away. How much time will it take the arrow to hit the target? How far below (or above) the bullseye will the arrow hit? Notice that the only thing different about this example than the previous one is that the arrow is shot an an upwards angle.

Since the initial velocity isn't purely horizontal or vertical, we need to calculate the components using trig.

       

Now, calculate the time needed to reach the horizontal distance of 20.0 meters...

            

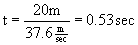
Notice it takes a little longer for the arrow to get to the target than in the previous example, because the horizontal velocity is a little less.

Now we can answer the last question, where does the arrow hit?

         

It hits 5.88 meters above the bullseye.

5. A grasshopper leaps at a speed of 3.0 meters per second, at an angle of 50 degrees above the horizontal.

(a) Calculate the horizontal and vertical components of the initial velocity.

(b) How much time will it take for the initial vertical velocity to decrease to zero, at the apogee of the grasshopper's flight?

(c) How much time will it take to land?

(d) How far away does it land?

(Assume the ground is level, and there is no air resistance.)

Additional Activities & Practice

6. Early every November, in southern Delaware, there is held a Punkin Chunkin Contest --- people use machines they have built to hurl pumpkins as far as possible. Why? Eternal glory for the winner. Suppose you build a catapult that launches a pumpkin at a 45-degree angle above the horizontal at a speed of 65 m/sec. How far away will the pumpkin land? (HINT: follow the same steps as Problem 5.) Watch the solution video.

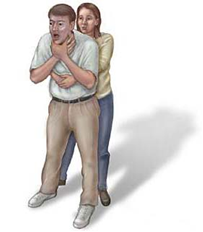
7. Once, long ago, I had dinner at a fancy restaurant with Cindy Crawford. This is before either of us was married. Suddenly, I began choking on a piece of chicken cordon bleu, which was ironic, because now I was turning blue myself. Cindy knew just what to do. She stood behind me, wrapped her arms around my chest and performed the Heimlich maneuver. The chunk of chicken was expelled, and landed 2.6 meters in front of me. My mouth is about 1.7 meters above the floor. If we assume the chicken was shot out of my mouth perfectly horizontally,...                 (a) How much time did the food take to hit the ground?                 (b) What was the food’s initial speed as it left my mouth? Watch the solution video.

8. “Bombardier” beetles protect themselves from predators by squirting out blobs of boiling-hot irritating fluid at the attacker. Some of these blobs having been observed leaving the beetle at 11 m/sec. Suppose a beetle shoots the fluid at a 45-degree angle above the horizontal. Assume air resistance is not important.

(a) Calculate the initial horizontal and vertical velocities of the fluid.
(b) How much time will it take the blob to reach its apogee, where the vertical velocity is zero?
(c) How much total time will it take the blob to land (assume the ground is level)?
(d) How far, horizontally, does the blob travel?

9. A cannon is fired at a 45° angle. At the instant the cannonball is at the top of its trajectory (the apogee) which of the following are equal to ZERO? We are ignoring air resistance, as usual.
CIRCLE ALL THAT APPLY
                (a)  the cannonball’s horizontal acceleration        (b)  the cannonball’s vertical acceleration
                (c)  the cannonball’s horizontal velocity             (d)  the cannonball’s vertical velocity
                (e)   the cannonball’s weight                             (f)  the cannonball’s mass

10. The World High Diving Championships were held on 25 Oct 2008 in Veracruz, Mexico. Steve Black of Australia was the winner. The diving platform was 25 meters above the surface of the water, and air resistance is not important.

(a) Assuming the diver launches straight outwards (no initial vertical velocity), how much time does the diver have to complete the twists and somersaults before entering the water?

(b) If the diver launched with an initial horizontal velocity of 0.75 m/sec, what is the diver’s horizontal velocity at the moment just before hitting the water?

(c) How far has the diver moved horizontally during the fall?

11. I went paintballing for the first time recently. The rules/liability form at the range said that no paintball guns were allowed to shoot balls faster than 283 feet per second. NOTE: 1 m = 3.28 feet

(a) Convert 283 feet per second into m/sec. Write out the full FL method setup.
(b) If a paintball is shot straight upwards at that speed, how much time will it take to reach its apogee? How high is the apogee? (Assume air resistance is not significant.)
(c) If you want the paintball to travel the furthest distance horizontally, at what angle should you shoot?
(d) If a paintball is shot at that angle, at that speed, what will be the horizontal and vertical components of its initial velocity?
(e) Part (d) continued..how much time will it take to reach its apogee? How much time will it take to hit the ground? How far away will it hit the ground?