Newton's Second Law of Motion
for translational motion
Newton’s Second Law expresses mathematically what, in words, seems like common sense. First, the harder you push on something, the faster it will accelerate. Secondly, the bigger the object (specifically, the more mass it has), the less it will accelerate.
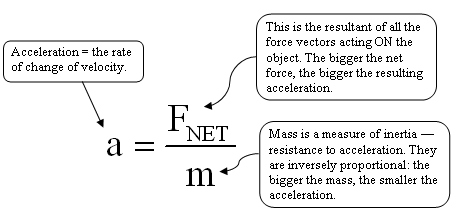
More commonly this is written as
Next to E=mc², this may be the most famous equation in all of science. Usually, it’s written as simply F=ma, but writing it this way obscures two important things to remember. First, the force is not any ol’ force. After all, there might be two or three (or eleven) different forces acting simultaneously on the mass m. There can only be one acceleration value at any one time, so the force in the equation has to be the vector resultant of all those forces, namely FNET. Second, I like to write a=FNET/m because this form of the relationship puts the things that are usually controllable (the forces and mass) together on one side of the equation, and the effect (the acceleration) on the other. Acceleration doesn’t cause a force; force does cause acceleration. Mass (inertia) resists acceleration.
Here's an experiment for you. Watch the video below, pausing the video when it says so you can think about the question asked.
From ,
we see that the unit of force must be the unit of mass times the unit
of acceleration. In SI, that would be 
,
which is the same as 
That's
a mouthfull, and because we’ll be talking about forces a lot, it’s
handy to have a shorter name. In honor of Sir Isaac Newton, the name
was chosen to be the Newton, symbolized with an N.
The English unit of force is called the pound. One pound is equal to 4.45N. (The abbreviation for the pound is lb, a shortened form of Latin libra, 'scales' or 'pound'.)
Newton's Second Law is a mathematical relationship, i.e. it's used for calculations. So let's see an example. Click the picture to watch the video.
In the example above, the force pulling the train was the friction between the wheels of the locomotive (which the steam engine was turning) and the rails of the track. Friction is only one of many different types of force we experience in our lives. Here's a list of the most common forces.
Examples of forces:
- FF = FRICTION = force due to a surface rubbing against another surface. The direction of the force is parallel to the surfaces, and is opposite the direction of the motion or attempted motion.
- FA = APPLIED FORCE = a force exerted by choice, such as a person pushing or pulling. The magnitude and direction of the force are up to the person exerting it.
- FN = NORMAL FORCE = the force of two surfaces pressing against each other. The force is perpendicular to the surfaces. (The word normal has a technical meaning here, synonymous with perpendicular.) The magnitude of the normal force is just enough to keep the two objects from passing through each other.
- FT = TENSION = the pull exerted by a stretched rope, string or chain. The direction is always a pull (not a push), and parallel to the rope/string/chain.
- Fg = WEIGHT, also known as the force of gravity. Direction is, by definition, downwards.
- FB = BUOYANCY = an upwards force due to a greater pressure on the bottom of an object than on the top, for an object immersed in a fluid.
- FD = DRAG = the force of resistance as an object moves through a gas (for example, air) or liquid (like water).
- FTH = THRUST = the force due to a rocket or jet engine ejecting hot gases.
- FL = LIFT = the force produced by an airplane wing or helicopter rotor. Lift and thrust are essentially the same principle (see the discussion of Newton’s Third Law of Motion) but the differing names are traditional.
If you know all the forces (including directions) acting on an object, you can determine the net force in two different ways you already know: either draw a vector diagram to scale, or use trigonometry and components.
Activities & Practice
to do as you read
1. Land on the Moon Play the Lunar Lander game, located at http://phet.colorado.edu/simulations/lunarLander/lunarlander.swf.
Your keyboard up/down arrow keys control the rocket engine thrust; the space bar toggles between full thrust and off (which I find easier to use.) The left/right arrow keys rotate the lander by firing tiny rocket engines
in a clockwise and counterclockwise pattern. Before hitting the “Start” button,
turn on the vectors by clicking in the selection box. The green vector
represents the lander’s velocity; the acceleration vector is shown
as a yellow vector. The programmers really got the physics correct in
this game. For example, notice that when you hit the right arrow (clockwise
rotation) the tiny rockets push clockwise to start the rotation, and
then quickly fire again in the opposite direction to stop the rotation
from continuing. Your goal is to achieve a score of at least 50 points;
score over 100 points earns extra credit, and the highest score earns
extra-extra credit. Email me a screenshot of your end-of-game screen showing your score. (How? Hit the 'PrtSc' key -- above the F11 key on my keyboard -- then open an email to me, and type Ctrl-V to paste the screenshot into the email. DON'T save the screenshot and make it an attachment --- then I have to open two things instead of one.)
2. A hyena pulls on a 12-kilogram carcass with a force of 40 Newtons. What is the acceleration of the carcass? Assume there's no friction between the carcass and the ground.
3. From 1947-1954, Dr. John Stapp, an Air Force officer, lead a series
of experiments on the effects of extreme accelerations on humans. He
himself was the subject of most of the tests, in which he was accelerated
in a rocket sled running on a long horizontal track at Edwards Air Force
Base, California. In his last test, in 1954, he accelerated from rest
to 632 miles per hour in 5.0 seconds.
(a) Convert 632 mile/hour into m/sec.
(b) Calculate the acceleration, a.
(c) The sled was 700 kg in mass. What must have been the thrust of the rocket
motor? Assume friction and air resistance are not important.
Read about John Stapp at the Edwards AFB website,
http://www.edwards.af.mil/history/docs_html/
center/other_testing.html and http://www.edwards.af.mil/
history/docs_html/people/stapp_biography.html
4. The Dodge Viper SRT10 can accelerate from rest to 27 m/sec in 3.8
seconds. Its mass is 1550 kg.
(a) What is the acceleration?
(b) What type of force is providing that acceleration?
(c) How strong must that force be? (I.e. how many Newtons?)
5. A hockey puck is sliding across the ice, gradually slowing down. Draw a free-body diagram for the puck, labeling all force acting on it.
6. The following statement of Newton’s First Law of Motion contains an error. Scratch out a single word and replace it with another word to fix the error.
An object at rest will remain at rest, and an object in motion will remain in motion with a constant speed, unless acted upon by an outside force.
Free-body Diagrams To help you visualize a situation, and to help you identify all the forces acting on an object, it is useful to draw a different kind of diagram, the so-called free-body diagram. Free-body diagrams are just sketches; don't bother with rulers and protractors. Here are the steps in drawing free-body diagrams:
- Draw a box or other shape to represent each object in the situation.
- Draw each force vector with its tail on the object feeling that force.
- Label each force vector with what type force it is (FN, for example) and its strength (in Newtons or pounds) if known.
- Draw ONLY force vectors — do not include velocity or acceleration vectors.
Here are a few examples.
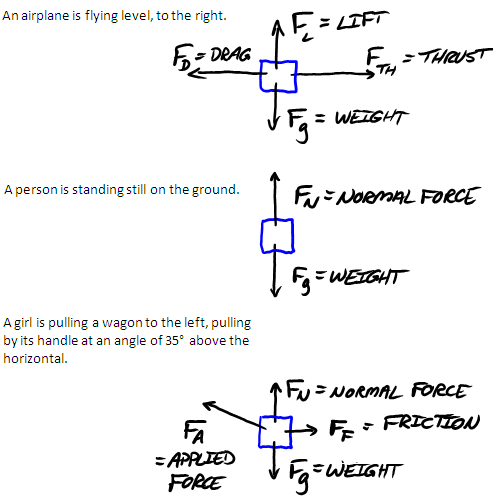
Notice that these are not great works of art. I didn't try to draw the airplane, person or wagon realistically, and you don't have to either. But the process of making the diagram helps you understand the situation and indentify ALL of the forces acting on the object.
Be careful! Free-body diagrams and vector diagrams are NOT the same thing! To find the net force, you still have to use components or a scaled vector diagram!
7. The simple act of crouching down and standing back up is not really so simple. Here's a video showning the process, including free-body diagrams at several moments: standing still, accelerating downward, stopping, staying crouched, accelerating upwards, slowing down, and standing still again.
You can sense these varying forces for yourself, even without a fancy electronic scale. Stand, and then crouch, all the while paying close attention to how hard your feet are pressed against the floor. The changes in force are most apparent if you do it quickly, but please be careful. Then stand up quickly. As your legs become straight again, you'll feel your feet press less hard against the floor, just as the scale revealed when Zoe stood up. If you do this rapidly enough, the normal force will become zero and your feet won't be touching the floor anymore. Physicists call this process jumping.
Additional Activities & Practice
8. Three sharks are pulling on a 180-kg elephant seal. Alice the shark pulls with 500 N of force in the direction 10° N of W. Bob the shark pulls with 400N toward 10° W of N. Charlie the shark pulls with 700N toward 40° E of S.
(a) Find FNET by drawing a vector diagram.
(b) Find FNET by using components.
(c) Calculate the acceleration of the elephant seal. (Ignore drag caused by the water.)
9. Three beetles are fighting over a 15 milligram scrap of leaf. Clyde pulls with a force of 7.0 mN in the direction 20° N of E; Delilah pulls with strength 13.0 mN in the direction 25° S of E; Edward pulls with 11 mN, directly southwards.
(a) Find FNET by drawing a vector diagram. Measure its magnitude and direction.
(b) Calculate the acceleration of the leaf scrap.
(c) Along comes Flora, another beetle. She pulls on the leaf too, so the net force is zero. How strongly, and in what direction, is Flora pulling?
10. Draw a free-body diagram for a ball thrown straight up in the air at four different times. Do NOT ignore air resistance.
(a) Just after the ball has left the thrower’s hand
(b) The instant the ball is at its apogee.
(c) As the ball is falling downwards, but slowly.
(d) As the ball is falling downwards, after faster than (c), so that the magnitude of the air resistance equals the ball's weight. (At this point, the ball has reached "terminal velocity".)
11. In the forests of the Pacific Northwest lives a community of Yeti, also known as Bigfoot1. In Yeti society, they measure length in a unit called an “ugg”, time in a unit called a “nnng”, and mass in a unit called “oooh”. By combining these units properly, what is a valid unit of force in the Yeti system?
Footnotes
1Not really.