Momentum

What is Momentum?  Momentum is, no doubt, a word you’ve heard before. It is a quantity proportional to an object’s velocity and also its mass (inertia). In other words, the bigger the object, and the faster it is moving, the more momentum it has. We'll use the letter p to stand for momentum, because m is already taken for mass.

Isaac Newton called momentum a “quantity of motion”, and I’ve also heard it described as “inertia in motion”. Both phrases convey a correct sense of what it is. You can also think of momentum as “punch” — how much impact would a moving object have if it ran into you.

As you probably noticed, momentum is a vector, because velocity is a vector.

Example What is the momentum of a 0.145-kg baseball when thrown at 40 m/sec (about 90 miles per hour)?

                   
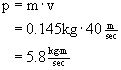
Notice the units used for momentum, .

1. What is the momentum of a Toyota Scion xB (mass = 1100 kg) traveling at 25 m/sec?

Example How fast would a fly (mass=12 mg) have to travel to have the same momentum as the baseball?

This question is asking for the velocity, so let's solve for v...

and plug in the momentum of the baseball and the mass of the fly...

So the fly would have to be moving at well over a thousand times the speed of sound to have the same momentum as a well-thrown baseball.

Conservation of Momentum  Why is momentum a useful concept? Because it is conserved. This means that, assuming there are no outside forces acting on the system, the total momentum of the system cannot change. This is especially useful for analyzing the collisions of objects. The total momentum before the collision is equal to the total momentum after the collision.

This is very useful for analyzing the following situations

• Recoil
• Collisions

but we'll talk more about that later.

Impulse  What if there is an outside force? Well, then the total momentum can change. Let's look at Newton's Second Law of Motion.

Let's replace the acceleration with the basic definition of acceleration.

Multiply both sides by — that moves it from the denominator on the right to the numerator on the left...

The quantity on the left, , is called the impulse. The quantity on the right, if we assume the mass of our object is not changing, is the change in momentum. The units of impulse are N·sec, equivalent to the units of momentum, kg·m/sec.

This last equation is called the impulse-momentum theorem. It is really just Newton's Second Law of Motion slightly rearranged. What it says is: You can effect a certain change in momentum by either exerting a large force for a short amount of time, or a small force for a long time. Here are some real-life examples:

• Jumping and landing: when you jump, how do you land? When your feet hit the ground, you bend your knees. Why? Because that allows you to stop your motion (change your momentum to zero) with a small force acting over a relatively long time.
• Airbags and crumple zones in cars. Here's an old video showing a crash test dummy being stopped with and without an airbag. Watch this video from the Insurance Institute of Highway Safety. Notice that the front of the car crumples up as it hits the wall. If the car were built as a very rigid structure that did not crumple, then the car would stop much more suddenly, and that would require much greater force. The airbag serves the same function for the person, stopping the person over a longer period of time, and with less force, than if the person were stopped by the rigid steering wheel or dashboard. Note that airbags are designed to work in conjunction with seatbelts. This video illustrates, is a disturbing way, that an airbag alone is not sufficient to stop you safely.
• Bike helmets, packing peanuts or any kind of padded packaging all serve the same purpose as airbags in a car.
• Eggtoss: if you want to catch a projectile egg that has been thrown at you, what is the best technique? GDS records
  

3. If the Toyota Scion xB accelerates from a stop to 25 m/sec in 8.0 seconds, what must be the net force on it?

4. If the Scion (traveling at 25 m/sec) then hits a brick wall and comes to a stop in 0.15 seconds, what is the force on it during the collision?

5. If the Scion (traveling at 25 m/sec) instead hit a huge cube of Jello that was mysteriously in the road, coming to a stop in 1.5 seconds, what is the force on it during the collision?

Example