Collisions
As mentioned in the "Momentum" notes, the Law of Momentum Conservation says that, if there is no outside force acting on a system, then the total momentum doesn't change. By "total momentum", I mean the vector sum, the resultant of the momentum vectors for all the individual objects that are in the system. This is useful because we don't need to know the details of the forces that are exerted during a collision or explosion.
![]()
There are two basic kinds of collisions. If two (or more) objects collide and stick together, that is called a completely inelastic collision. If the objects collide and do not stick together, that is an elastic collision. (The full definition of this requires that we talk about energy, which we haven't yet.)
An explosion can be thought of as a completely inelastic collision in reverse. Instead of separate objects coming together and becoming one object, in an explosion one object turns into multiple objects flying apart.
to do as you read
Example 1 A 10,000-kg railroad car, rolling at 4 m/sec, collides with another, identical car, that is at rest. The two cars couple together. What is their (combined) velocity after the collision?
Let's find the total momentum before the collision. Call the two cars A and B.
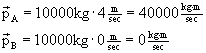
So the total momentum is 40000 kg·m/sec, and this is equal to the total momentum after the collision, also. Because this is a completely inelastic collision, there is only one object afterwards, the two-car mass of 20,000 kg.
![]()
1. A skateboarder (mass=50 kg) is coasting on a level track at 3.0 m/sec. A puppy (mass=15 kg) with no initial velocity jumps onto the skateboard. What is the velocity of the skateboard just after the puppy lands?
Example 2 A 10,000-kg railroad car, rolling at 4 m/sec, collides with another, identical car, that is moving at 6 m/sec in the opposite direction. The two cars couple together. What is their (combined) velocity after the collision?
Let's find the total momentum before the collision. Call the two cars A and B. Because the cars are moving in opposite directions, we have to assign one of the directions a negative sign. Let's make that car B's direction.
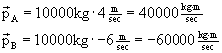
So the total momentum is -20,000 kg·m/sec, and this is equal to the total momentum after the collision, also. Because this is a completely inelastic collision, there is only one object afterwards, the two-car mass of 20,000 kg.
![]()
The two coupled cars are traveling at 1 m/sec, in the direction car B was going originally.
2. A truck (mass 8000 kg) travelling at 25 m/sec, has a head-on collision with a car (mass 1200 kg) travelling at the same speed in the opposite direction. The two vehicles are mangled together as a single mass after the collision. What is the post-collision velocity of the vehicles?
Example 3 A 10,000-kg railroad car, rolling at 4 m/sec, collides with another car, mass 15,000 kg, moving in the opposite direction. The two cars couple together, and after the collision the two coupled cars are at rest. How fast was the 15,000-kg car moving before the collision?
After the collision, the cars are at rest, so the total momentum is zero. Therefore, the total momentum before the collision is also zero. Car A has momentum of 40,000 kg·m/sec before the collision, so car B must have had the same momentum, only in the opposite direction.
![]()
3. An astronaut (mass, with spacesuit = 110 kg) is floating outside the space shuttle, at rest, and the tether (rope) comes disconnected. The astronaut has a 5 kg air tank, and throws it away at 4 m/sec. (a) In what direction should the astronaut throw the tank, so she will move towards the shuttle? (b) How fast will she move?
Example 4 Two ice skaters are on a totally frictionless frozen lake. Big Bob has a mass of 100 kg; Little Lester's mass in 60 kg. They are at rest, but then Little Lester pushes against Big Bob. Big Bob slides off at a speed of 0.3 m/sec. How fast is Little Lester moving?
This is a recoil problem. The total momentum is zero, because that was their momentum before the "explosion". Bob's momentum afterwards is...
![]()
Because the total momentum is zero, Little Lester must have the same momentum as Bob, only in the opposite direction, so...
![]()
4. If you could gather all the people of the world in one big field, and ask them all to jump up at the same time, how much would the velocity of the Earth change? This will require you to estimate the mass of people on Earth, and the typical velocity of a jump.
Example 5 Two railroad cars, traveling in opposite directions, have a head-on collision. Car A (25,000 kg) is moving 5.0 m/sec, and car B (10,000 kg) is moving at 4.0 m/sec. After the collision, the cars do NOT couple together. After the collision, car A is moving with speed 1.0 m/sec in its original direction. How fast, and in what direction, is car B moving?
Call the original direction of Car A the positive direction. Then the momenta of the the two cars prior to the collision are...
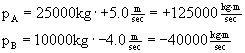
The total momentum, therefore, is
![]()
This is the total momentum after the collision as well. Car A, after the collision, has momentum
![]()
So Car B must have enough momentum so the total adds to +85,000 kg·m/sec. In other words, car B must have +60,000 kg·m/sec. Now we can calculate its velocity...
![]()
5. Two carnival bumper cars are traveling in the same direction. Car A (total mass 100 kg, traveling at 3.0 m/sec) catches up to and rams Car B (total mass 90 kg, traveling at 2.0 m/sec) from behind. After the collision, Car A is traveling in the same direction as before, but slower (1.5 m/sec). How fast is Car B moving?
Example 6 All of the previous examples were 1-dimensional: the motion was along a single straight line. Here is a 2-dimensional situation...
A car driving at 20 m/sec to the north enters an intersection. Unfortunately, at the same time, a pickup truck traveling at 15 m/sec to the west runs the red light on the cross street and crashes into the car. The two vehicles are mashed together as a single object. In what direction, and with what speed, do they move immediately after the collision? The car's mass is 1200 kg; the mass of the truck is 2200 kg.
Before the collision
The momentum of the car is
and the truck's momentum is
The total momentum is the resultant (vector sum) of these two momenta. Because these are purely in the north (+y) and west (-x) directions, the resultant can be found using the pythagorean theorem and the arctangent.
The magnitude of the resultant is
and its direction is
mathematical, if we believe the arctangent function, which we should never do without double-checking. In this case, gthe resultant is in the second quadrant, so the arctan function is lying to us. The true direction is 180° opposite, which is 144° mathematical, or 36° N of W.
After the collision
The total momentum after the collision is 40800 kg·m/sec in the direction 36° N of W. This is a completely inelastic collision, so the single post-crash mass of 1200kg+2200kg = 3400kg must be moving in the direction 36° N of W, with a speed of
Friction with the road is an "outside force" which will quickly bring the wreckage to a stop. What we calculated above is the velocity the instant after the collision.
Additional Questions
7. If Mars were to collide with the Earth, and they stuck together, how much would the velocity of Earth change? Assume the mass of Earth is 5.34x1024 kg, and the mass of Mars is 6.4x1023 kg. Assume the Earth is stationary to begin with, and Mars hits it at 35 km/sec.
8. A truck (12000 kg) driving down the road at 20 miles per hour hits a car traveling in the opposite direction. The car's mass was 4000 kg. Immediately after the crash the two come to a stop (not because of friction, but because of the crash). How fast was the car traveling before the crash?
9. A car and a truck, identical to and moving at the same speeds as in the previous problem, collide. In this collision, however, the car is initially traveling west, and the truck is going to the south. When they collide they mangle together. How fast and in what direction are they moving (together as a single mass) immediately after the collision?
10. Three hockey players are fighting in a pile, and the ice is so slippery that friction is not significant. They push off against each other, and each goes sliding outwards in a different direction. Abigail (mass 55 kg) is slides at 0.95 m/sec in the direction 25 degrees azimuth. Beatrice (mass 62 kg) slides at 1.2 m/sec at 130 degrees azimuth. In what direction, and at what speed is Clarissa (mass 65 kg) sliding?