Gravitation

Introduction Recall, way back when we first introduced the concept of weight (which is the force of gravity, in contrast to mass, which is a measure of an object's inertia), we said that the weight is given by this equation:

where m is the mass of an object, and g is the gravitational field strength at that location. On Earth, g is 9.8 N/kg, on Mars it's 3.7 N/kg, etc. If gravity is the only force acting on an object (in other words, the object is falling) then the object will accelerate at 9.8 m/sec² if on Earth, and 3.7 m/sec² if on Mars. Because of this, we have often called g the "acceleration due to gravity", but do always remember that it's the acceleration only if the object is in free fall.

What we didn't discuss at that time was this question: "Why is the gravitational field strength different on different planets?" Like every force, gravity is an interaction between separate objects. Gravity is an effect caused by mass and depends on the mass of both of them. The more mass in each, the stronger the gravitational tug. But gravity must also get weaker with distance, otherwise you would be pulled more strongly to all the objects in the universe more massive than Earth (of which there are many) than to the Earth itself.

The description of the previous paragraph boils down to this equation:

where m₁ and m₂ are the two masses, and r is the distance between their centers. G is the universal gravitational constant, which describes how strong gravity is, in general, rather than the strength of gravity at any one particular place.

 

Activities & Practice
to do as you read

1. The equation at left is Isaac Newton's Law of Universal Gravitation, figured out by him in 1666. We've talked quite a bit about Newton's life and work during class. Listen to this podcast from NPR's Talk of the Nation about a lesser-known aspect of Newton's later life. (If the link to NPR doesn't work, here's an archive copy.)

The Universal Gravitational Constant, G

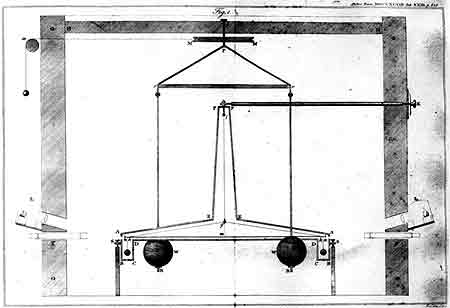
Imagine setting up an experiment in a lab. You take two 1-kilogram masses and set them 1 meter apart from each other. Then you measure the force of gravity between them, which is tending to pull them together. That is essentially what Henry Cavendish did in 1797. Now, I'm leaving out a lot of messy details. The force of gravity between such small objects is going to be extremely small. How can you possibly measure it? Cavendish used a torsion balance, which had been invented by John Mitchell but bequeathed to Cavendish when Mitchell died. Two metal balls were attached to the ends of a rod, and the rod suspended from its center by a thin fiber. Two other larger, metal spheres were placed close to the balls on the suspended rod, so that the gravitational tug would tend to twist the hanging rod. (Click on the diagram for a larger version. Notice that one of the large metal spheres is in front of the hanging rod from our perspective, and the other is behind.) Cavendish carefully measured how much torque was needed to twist the fiber. The whole thing was placed in a sealed container so no air currents can disturb it. By observing how much the rod twisted when the large spheres were brought close to the small ones, the force of gravity between them could be calculated. Because the masses and the distances were known, G could be calculated. Cavendish came within 2% of the modern value, found by using techniques very similar to Cavendish's (but updated with modern technology). Our current best estimate for the value of G is

2. What is the gravitational force between two 1-kilogram masses separated by one meter?

3. What is the gravitational force on a 3-kilogram baby from a passing airliner (mass 250,000 kg) flying overhead at an altitude of 3000 meters?

4. What is the gravitational force from the planet Mars acting on that same 3-kilogram baby, at a typical distance of 200 million kilometers? The mass of Mars is 6.4x10²³kg, about 1/10th the mass of Earth.

EXAMPLE

What is the gravitational force between an adult (60 kg) and a baby (3 kg) when they are 2 meters apart?

Watch solution video.

Let's compare the two equations we have for the gravitational force:

If we take m₁ to be the mass of an object (what in the first equation we called simply m), and m₂ to be the mass of the planet, then g must be equal to

The gravitational field strength, g, depends on two things: the mass of the planet, and the distance to the center of the planet.

5. When Cavendish published the results of his experiments, he did not consider measuring G to be his most important result. Instead, his measurement of G allowed him to calculate the mass of the Earth. He was, in a sense, "weighing the Earth". Given G, and the facts that the radius of the Earth is 6378 km, and g at the surface of Earth is 9.8 m/sec², calculate the mass of the Earth.

6. What is the gravitational field strength at the height of a space shuttle orbit, 400 km above the surface of the Earth? (Hint: remember, r is the distance to the center of the Earth.)

Additional Activities & Practice