Friction
Introduction You already know what friction is, from your everyday experience. Some people call it "traction". If you try to slide a box across a floor, you know that it'll take some effort to get it going, and keep it going, because of the friction between the box and floor. It's easier if the floor is smooth, and easier still if the box has wheels. You may have also noticed that usually it's easier to keep the box moving, once it's moving, than it was to get it started.
Here's a song about friction.
What causes friction? That isn't a trivial question to answer. First, realize that two surfaces that are touching are not really touching across the entire area that appears to be touching, because the surfaces are rough.There is no such thing as a perfectly flat surface. Seen through a high-power microscope, a typical surface looks like the following pictures. (These are, left to right: a typical metal surface, polished metal, wood, and porcelain.)

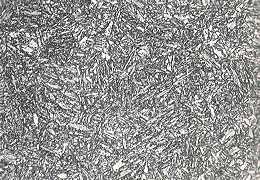

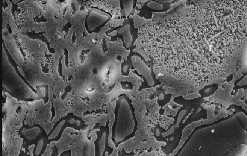
So, two surfaces in contact look like this, on a microscopic level:
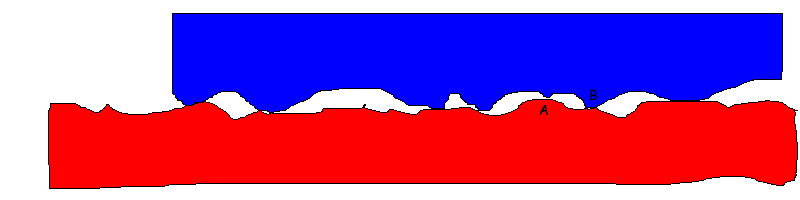
Notice that the two surfaces are only really touching at a few places. At these places of true contact, friction can happen for a couple of reasons:
- Wear. A "mountain" on the lower surface (like point A) gets in the way of an upside-down mountain on the top surface (like point B). Imagine the blue object being pushed to the left. As the top surface tries to move leftward, either the top object will have to ride up or deform a little to allow the obstructions to pass each other, or the surfaces (like points A or B) will have to break off. This is the origin of the idea of "wear and tear", describing how objects change after much usage. A knife, for instance, will "lose its edge" as the atoms along the sharp edge get removed, making it less sharp.
- Chemical bonds. The atoms of one object chemically bond with atoms
from the other object. For the top object to move, those bonds have
to be broken. This source of friction is less important than wear in
most situations, but can be important when the two materials have a
chemical affinity for bonding, or when the materials are the same,
and the surfaces are very clean.
Activities & Practice
to do as you read
1. Play with this simulation of what's happening at the microscopic level that causes friction.
Static Friction vs Kinetic Friction If
two surfaces are in contact and are not sliding, then the chemical bonds
have enough time to
develop
at
many
places,
and the upside-down-mountains in the upper object are fully seated in
the valleys between the mountains of the lower object. So, for most materials,
the friction needed to break free from a stopped position is greater
than
the friction needed to keep moving after movement starts. The frictional
force when the surfaces are not sliding relative to each other
is called static
friction, FFS. If you push lightly
on a box resting on the floor, it won't move. Push a little harder, and
it still won't move.
Apparently, the static frictional force can adapt — it can
be any value from 0 Newtons, up to some maximum value, which we'll call
FFS,Max. When
the surfaces are sliding,
we call that friction kinetic friction, FFK.
2. Play with this simulation of Motion and Forces, working through all four sections. In each case, turn ON the display of the force vectors using the checkboxes.
The Role of the Normal Force In both
cases, static and kinetic, the harder the two surfaces are pressed into each
other (in other words, the normal force, FN), the greater the
frictional force.
The Role of the Materials How much
friction there is also depends on what the two objects are made out of.
A hockey puck experiences less friction sliding over ice than it would
if, say, the rink were coated with rough sandpaper. It is convenient
to characterize the "slipperyness" or "stickyness" of two materials rubbing
against each other with a number. A fancy word for "number" is coefficient.
Putting the factors together mathematically. Recapping the above discussion...
"Apparently, the static frictional force can adapt — it can be any value from 0 Newtons, up to some maximum value, which we'll call FFS,Max."
![]()
"In both cases, static and kinetic, the harder the two surfaces are pressed into each other (in other words, the normal force, FN), the greater the frictional force." In other words, the maximum static friction, and the kinetic friction, are both proportional to the normal force. The proportionality constants are, respectively, the coefficient of static friction (µs) and the coefficient of kinetic friction (µk). The greater the µ, the more "sticky" the surfaces are.
![]()
![]()
"The friction needed to break free from a stopped position is greater than the friction needed to keep moving after movement starts."
For
most materials, ![]()
3. Push a filing cabinet in this friction simulation. Click-n-drag the cabinet to apply force to it, and see the static friction oppose you until you push hard enough. There is a live free-body diagram at the upper-right corner. Turn on the applied force and other graphs. Experiment.
Here are a few specific questions:
(a) How much force does it take to get the refrigerator moving?
(b) How much force does it take to keep the refrigerator moving at a constant speed?
(c) If you double the mass of the refrigerator from 200 kg to 400 kg (use the "Additional Controls" button at the lower right), what happens to your answers to (a) and (b)?
Coefficients of Friction
The coefficients of static and kinetic friction are determined by experimentation. Take two objects, measure the normal force between them and the applied force needed to (a) start the sliding, and (b) keep the sliding going at constant velocity.
Coefficients of friction for myriad materials can be found in standard reference books used
by scientists, engineers and designers.
Example A 25-kilogram cardboard box full of books is sitting on a level concrete floor. A person pushes the box sideway with a force of 47 Newtons.
(a) What is the coefficient of kinetic friction?
(b) If 11 kilograms of books are removed from the box, how much force will now be required to push the box across the floor?
(a) The box weighs F = m · g = 25kg · 9.8N/kg = 245N.
Since the box is moving with constant velocity, the net force is zero and FA = FFK
Solve the friction equation for the coefficient of friction: µk = FFK / FN = FA / Fg = 47N / 245N = 0.19
(b) The box now is only 14 kg in mass, and its weight is Fg = m · g = 14kg · 9.8 N/kg = 137 N. The result of part (a) says that, for this particular combination of cardboard and concrete, the friction will be 19% of whatever the normal force is.
FFK = µ · FN = 0.19 · 137N = 26N
Implications for Your Life
If you are ever trying to push a box across a floor, don't let your applied force have a downward component. Doing so is inefficient, for two reasons. First, the downward component of your push just presses the box harder into the floor. In other words, it increases the normal force, which isn't your goal. Secondly, that increased normal force increases the friction. Instead, push perfectly horizontally. Better yet, pulling with some upward component of force will reduce FN and therefore reduce the friction.
| If you are buying a car, and are choosing between a car with ABS brakes and one with non-ABS brakes, get the one with ABS. ABS stands for Anti-Lock Braking System. Let's say you are driving, and a child runs out into the road directly in front of you. Most drivers in that dire situation will slam on the brakes, stepping on the brake pedal as fast and hard as they can. In a non-ABS car, the brakes will lock the wheels, and the car will skid. Kinetic friction between the tire and the road will slow the car. But kinetic friction is less than the maximum static friction, so it would be better to not skid. Instead, you want to apply the brakes as hard as you can up to, but not quite, the point where the wheels lock and the tires skid. Good drivers do this by rapidly pumping the brake pedal, several times per second, but in a sudden panic even good drivers can forget. ABS brake systems pump the brakes for you (typically 10 times per second), preventing a skid and stopping the car in a shorter distance. | 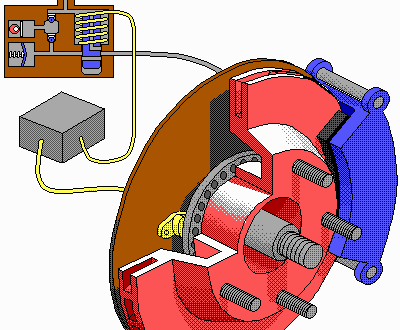 |
Additional Activities & Practice
4. A particular box, weighing 20. N, is being pushed on a horizontal floor. If requires a 7.0-Newton horizontal push to "break" the static friction, and 5.0 Newtons to keep it sliding with a constant velocity. Solution
(a) What is the coefficient of static friction?
(b) What is the coefficient of kinetic friction?
(c) If more stuff is put into the box, bringing its total weight up to 1.0x10² N, what will the maximum static friction and the kinetic friction now be?
5. Car tires are designed to have high coefficients of friction. Let's say a particular tire, on typical asphalt, has µk = 0.70 and µs = 0.80. Let's say four of these tires are on a car that is 1200 kg in mass. Solution
(a) What is the weight of the car?
(b) What is the normal force between each tire and the road?
(c) What is the maximum static friction acting on one tire?
(d) If the car is skidding, what is the friction acting on one tire?
6. A book with mass 0.30 kg is pressed into a wall by Mr. Regester, pushing purely horizontally. The coefficient of static friction is 0.15. The book is not moving. Solution
(a) Draw a free-body diagram for the book. (Hint: there are 4 forces acting on the book.)
(b) What is the net force acting on the book?
(c) What is the weight of the book?
(d) What is the static friction force acting on the book?
(e) What is the minimum force Mr. Regester must exert horizontally, to keep the book from sliding down the wall?
7. A 50.0-kilogram wooden box is placed on the floor. You push sideways on the box. At first it doesn’t move, but when you push hard enough (140 Newtons) it starts to slide. To keep it sliding with a constant velocity, you only have to push sideways with 120 Newtons of force.
(a) What is the weight of the box?
(b) What is the coefficient of kinetic friction?
(c) What is the coefficient of static friction?
(d) If you put 150 kg of bricks in the box, how hard do you have to push sideways on the box to get it to start moving?
(e) If instead of pushing sideways on the box you decide to push at a sideways and downward direction on the box, would you have to push with more, less or the same force in order to get the box sliding?
8. What are the names of the two kinds of friction we have discussed?
What kind of friction is there between the tires and the road, when a car is skidding?
What kind of friction is there between the tires and the road, when the car is starting or stopping normally, without skidding?
Which will stop you in a shorter distance in an emergency? (A) stepping hard on the brake pedal, but just short of skidding, or (B) stepping on the brake pedal as hard as you can, causing the car to skid.
9. A 950-kg car is driving on a level road. The coefficient of static friction between the tires and the road is 0.85, and the coefficient of kinetic friction is 0.75. The car is travelling at 22 m/sec.
(a) What is the magnitude of the normal force?
(b) The driver slams on the brakes, locking the wheels and causing a skid. Draw a free-body diagram of the car during the skid. Assume the car is skidding to the left.
(c) What is the magnitude of the friction force?
(d) What is the resulting acceleration of the car?