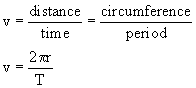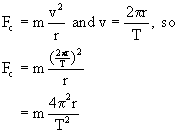Centripetal Force
Introduction As you know, the inertia of an object tries to keep it moving with a constant speed in a straight line. In order for an object to turn direction, there must be a component of force perpendicular to its velocity. If the force is entirely perpendicular to the velocity, the object will travel in a circle.
A sideways force acting on an object, causing it to move in a circle, is called a centripetal force.
The centripetal force is not a new kind of force. The label "centripetal" refers to any force that keeps something turning in a circle. That force could be tension, gravity, friction, electrical attraction, the normal force, or any other force.
Examples
- Whirling an object on the end of a string — the centripetal force is the tension of the string.
- Planets orbiting the Sun— the centripetal force is gravity.
- Electrons orbiting the nucleus — the centripetal force is the attraction of the negatively-charged electrons to the positively-charged nucleus (the electromagnetic force.)
- A car turning a corner — the centripetal force is friction. Imagine trying to turn a corner if the road is icy. The lack of friction prevents the car from changing direction, and you go in a striaght line instead.
- An airplane turning in a level circle — the horizontal component of the lift provides the centripetal force. The lift is not purely vertical because the wings are banked.
- The ball bearing
demonstration done in class— the centripetal force
is the normal force of the ring pushing on
the ball.
The word "centripetal" was coined by Isaac Newton from the Latin words centrum, "center", and petere, "go towards, seek". It is a force towards the center of the circle. This is in contrast to the erroneously-named centrifugal force, which describes the sensation of inertia one feels when being twirled in a circle. Because your inertia is "trying" to make you go in a straight line, tangent to the circle, you feel like you are being pulled outwards. The root -fug- in "centrifugal" comes from the Lain fugere, "to flee". Have you ever been in a car that's taken a curve a little too fast? You know that pull to the side you feel? What you are feeling is your inertia, wanting you to go in a straight line, which would carry you farther from the center of the turn. The only actual force, though, is whatever force is pulling you inwards, the centripetal force. In the fast-turning car, that centripetal force is provided by the friction of your butt on the seat, the seat belt and, if the turn is really radical, maybe the side of the car door pressing on your side. That's why some cars have grab handles hanging down from the car roof, next to the door, for you to hold onto when the car is making a sharp turn.
Here is a small presentation on Centripetal Force in Everyday Life and the Movies.
Here is a video clip from the 1979 James Bond movie Moonraker, in which Bond endures a harrowing ride on a centrifuge, a spinning device used to simulate gravity. Actual centrifuges, like in the movie, are used to train astronauts and fighter pilots how to withstand extreme acceleration. Small, tabletop centrifuges are used in labs worldwide to (for example) separate blood cells from the blood plasma (the liquid part of blood).
The 1968 movie 2001:A Space Odyssey envisioned what humans would be doing in space in the year 2001. Considering the U.S. was on the verge of sending humans to the Moon, just ten years after launching its first satellite, most people thought that by the start of the 21st century we would have colonies on the Moon and Mars and giant space stations in orbit, housing hundreds of people. The space station in this movie clip is a giant doughnut, spinning to produce simulated gravity so the people inside can walk around and work normally. People walk around with their heads pointed toward the center of the circle. The centrifugal force (which is really just inertia) acts like artificial gravity.
Activities & Practice
to do as you read
1. What type of force is providing the centripetal force in these situations?
(a) a moon orbiting a planet
(b) you running on a circular track
(c) the “Gravitron” carnival ride (wherein you stand in a
circular room that spins, and you feel stuck onto the wall.)
2. Draw an overhead view of a person twirling a rock on the end of a string. Imagine the string breaks. Draw the path that the rock follows.
3. Name as many English words as you can that contain the Latin root -fug-, refering to escape or fleeing? Do the same for English word with the -pet- root, meaning 'to seek'.
Magnitude of the Centripetal Force
The force needed to keep an object of mass m traveling in a circle of radius r at speed v, is given by this equation:
The quantity ac = v²/r is called the centripetal acceleration.
To a person going in a circle, the centrifugal force feels like some mysterious pull to the side, with a magnitude equal to the actual centripetal force. The magnitude of the centripetal acceleration is the g of "artificial gravity" that the person experiences.
Where the heck did these equations come from?! Watch this video, which derives them, and which will also help you understand the equations below.
 (Click image to start.)
(Click image to start.)
The period of revolution, T, is the amount of time needed for the object to travel one full circle.
The relationship between T, v and r is the basic definition of average speed.
Plugging this into the centripetal force equation yields an alternate form, where the magnitude of the centripetal force is given in terms of period rather than velocity.
The quantity ac = 4π²r/T² is the centripetal acceleration.
Since the period is the amount of time needed for one revolution, then the reciprocal of the period is the number of revolutions completed per unit time. This is called the frequency. In equation form,
If period is measured in minutes, then the frequency is the number of revolutions per minute, or as most people say it, RPM. If period is measured in seconds, then the frequency is revolutions per second, sometimes phrased as "cycles per second". Since seconds is our standard SI unit of time, "cycles per second" has been given a shorter name, the Hertz, abbreviated Hz. This name is in honor of Heinrich Hertz, 19th-century physicist and pioneer of radio communications, where the concept of frequency is very important.
4. What is the force needed to keep a 50-kilogram person moving in a circle of radius 2 meters and a period of 4 seconds?
5. What happens to your answer to 4, if...
(a) the period was doubled, but the radius and mass weren't changed?
(b) the mass was doubled, but everything else was unchanged?
(c) the radius was doubled, but the velocity and mass weren't changed?
(d) the velocity was doubled but the radius and mass weren't changed?
6. What is the magnitude of the centripetal force keeping the Earth in orbit around the Sun? (Note: The mass of Earth is 5.98x1024 kg, and the radius of the orbit is 150 million kilometers.)
7. In the movie 2001: A Space Odyssey (watch the video clip, above), the space station appears to be rotating with a period of about 40 seconds. Assuming the intent of the imaginary space station designers was to create "artificial gravity" of 1 g, at the outer edge of the station, was must be the radius of the station? (HINT: in other words, the centripetal acceleration = 1 g. Solve for r.) SOLUTION VIDEO
Example In the above video clip from Moonraker, just before Bond disables the centrifuge with the gun hidden in his coat sleeve, the control panel indicates a (centripetal) acceleration of 12 g's. Inside the centrifuge car, Bond would feel 12 times "heavier" than normal, as if gravity were suddenly twelve times stronger. Looking at the video frame-by-frame, at this point it takes the centrifuge 31 video frames to complete one revolution. (The frame rate is 30 frames per second.) An earlier frame, when Bond and his host enter the centrifuge chamber, shows the radius of the centrifuge is about 5.3 times Bond's height, which if we assume Bond is 6 feet tall, gives a radius of about 9.7 meters.
Are these numbers consistent? Did the movie-makers really have a centrifuge producing 12 gees of centripetal acceleration, or was it faked? Let's do some calculations...
The period, T, is 31 frames, or 1.03 seconds. 12 g = 120 m/sec².
With this period and radius, let's calculate the centripetal acceleration and see if it's about 120 m/sec².
ac = 4π²r/T² = 4π² (9.7m) / (1.03 sec)² = 360 m/sec².
This centripetal acceleration is about 36 g's, way above the 12 gees indicated on the control panel in the movie clip.
The radius of the centrifuge is the number we know least well, since we don't know the distance of the camera from Bond in the reference frame used to set the scale. So let's calculate the radius needed to give a centripetal acceleration of 12 gees if the period is 1.03 seconds.
Solving ac = 4π²r/T² for r gives us r = ac·T² /(4π²)
Plugging numbers into this yields r = ac·T² /(4π²) = 120 m/sec² · (1.03 sec)² / (4*3.1416²) = 3.2 meters, which is not even twice Bond's height.
Clearly the filmmakers sped up the spinning of the centrifuge to make it look more dramatic. That's not surprising, of course — they weren't making a documentary.
A Horticultural Surprise: What if you planted grass seed in a pot of soil that was spinning? How would the grass grow differently? Make a prediction NOW, then watch this video...
The seedlings grew with the blades of grass bent inwards. The spinning creates "artificial gravity", just like the space station in 2001: A Space Odyssey. Grass grows upwards, away from gravity, so if the artificial gravity has an outwards component, the grass will grow with an inwards tilt.
Analysis of a Salad Spinner
Additional Activities & Practice
| 8. Physics Trick: Get a wire clotheshanger and bend it into a diamond shape. Hang the diamond vertically, from one index finger, with the round hook at the bottom. Balance a penny on the end of the upward-pointing end of the wire of the hook. Now, see if you can twirl the whole thing in a vertical circle around your finger without the penny falling off. It's especially impressive if you can stop twirling with the penny still balanced on the wire. |  |
| 9. Make a prediction: Imagine a lit candle sitting near the edge of a rotating platform. As the candle revolves, what is the reaction of the candle flame? Specifically, will the flame be straight up, as it would be if it weren't moving, or does it lean in some particular direction. If the latter, which direction? There is a shield around the candle, so there is no "wind" blowing on the candle. This question is purely about the effect of the revolution itself. Write your prediction, including an explanation for your choice. Then watch the video to the right. Was your prediction correct? If not, rethink it and try to figure out how your reasoning was off. |  |
10. The University of Arizona, Steward Observatory Mirror Lab makes large concave telescope mirrors by melting the glass inside an oven that is itself on a large turntable. The mirrors they make are up to 8.4 meters in diameter. When the molten glass is spun, it flows outwards, making a parabolic shape needed for telescopes. Still turning, the temperature is lowered, solidifying the glass in that shape. Here's a time-lapse video of the process, and another showing the view inside the rotating oven. Here is a series of three videos showing, and explaining, an experiment with a container of water spinning. The third video requires a knowledge of calculus, so consider that one optional. Spinning Water: The Experiment |