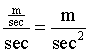Acceleration
Definition We can define acceleration as the rate of change of velocity. Let's break this phrase down into its parts...
- rate means "per time interval" or "divided by time interval"
- change of velocity means the velocity minus the initial velocity (the velocity at some defined "start" time)
In mathematical symbols, ![]() .
The bar over the a means this is really the average
acceleration over the time interval Δt.
In most problems we will be discussing, the acceleration will have a
constant value, so we'll often just write
.
The bar over the a means this is really the average
acceleration over the time interval Δt.
In most problems we will be discussing, the acceleration will have a
constant value, so we'll often just write
EXAMPLE: Let's say you want to buy a car, a Chrysler Curmudgeon. The ads for the car say it can go from "zero to sixty in five seconds." This is a way of describing the car's acceleration. The velocity units are, in the U.S., almost always miles per hour. Let's apply the mathematical definition of acceleration...
What this means is that, every second, the car gains 12 mi/hr in speed compared to the previous second.
If we solve this equation for Δv, we get ![]()
EXAMPLE: From rest, after 1 second the accelerating Chrysler Curmudeon is traveling at 12 mi/hr; after 2 seconds, 24 mi/hr; after 3 seconds, 36 mi/hr, et cetera.
Lastly, we can solve the equation for the time: ![]()
EXAMPLE: As we calculated above, the Chrysler Curmudeon accelerates at 12 mi/hr/sec. If it could maintain that acceleration, how much time would it take to get to 100 mi/hr?
ANOTHER EXAMPLE
If we graph velocity as a function of time for an object starting from rest, and accelerating with constant acceleration, the graph will look like this:
Remember the definition of the slope of a line? Usually
it is given as ![]() .
Compare this with the definition of acceleration and the graph above,
and you'll realize that the acceleration is the slope of the graph
of v(t).
.
Compare this with the definition of acceleration and the graph above,
and you'll realize that the acceleration is the slope of the graph
of v(t).
What if we want to calculate how far an accelerating object moves?
Recall from the notes on Graphing Motion, that the area under the graph of v(t) is equal to the distance traveled. So, if an object is accelerating from rest, how far will it go? We need to find the area of the triangle in the graph above. For a triangle, area=(1/2)base·height, so...
But
, so we can replace the
with
...
If an object is accelerating with a constant a, but with an initial velocity vo, how far will it go? See the v(t) graph above. The area under the graph is a triangle plus a rectangle, and so
In the above acceleration examples involving the Chrysler Curmudeon, I used units of miles per hour per second. Usually, though, we will be measuring velocity in meters per second, and so acceleration will be in meters per second per second. Written with division signs instead of pers, that is...
Activities & Practice
to do as you read
Play with the Moving Man simulation. It displays x(t), v(t) and a(t) graphs for the man at the top of the screen. You can control the man by clicking and dragging him, by typing in a value for his position, velocity, or acceleration, or by dragging the position, velocity and acceleration sliders. Hit the 'Help' button in the lower right corner. Play with the simulation for a while, just experimenting until you feel confident with the controls. Then try to do each of these tasks only by dragging the man:
(a) Make the man move with constant velocity to the right.
(b) Make the man move with constant velocity to the right, faster than in (a)
(c) Make the man move to the left with the same speed as in (b)
(d) Make the man move with constant acceleration.
Play in the "Arena of Pain". Use the green control arrow to move the ball. The arrow can represent either the position (relative to the center of the "arena"), the velocity, or the acceleration vector of the ball (R, V, or A, respectively) depending on which you have selected. Practice for a while with the different options. Your objective is to navigate to the goal through the most difficult level ("arena of pain") using (a) the V control arrow and (b) the A control arrow.
Acceleration Due to Gravity, g The symbol a represents an acceleration, any acceleration. That could be the acceleration of a cat chasing a rabbit, or a rocket taking off, or a wagon being pushed by a little kid. We will be talking very often about falling objects. Falling objects also accelerate, due to the force of gravity (weight) pulling on them. It turns out that, if air resistance is absent or insignificant, all objects fall with the same acceleration. What that acceleration is depends on what planet you're on. On Earth, it's about 9.8 m/sec², or 32 ft/sec². (It actually varies a tiny bit from place to place on the Earth. On other planets, it can be completely different: on the Moon, it's 1.6 m/sec².) Because it comes up so often, the acceleration of falling objects is given a special symbol, g.
Some Examples
VIDEO EXAMPLE: From San Francisco's Golden Gate Bridge, you drop a heavy rock. How far does the rock fall in 3.0 seconds? How fast is it moving after 3.0 seconds? VIDEO EXAMPLE: From San Francisco's Golden Gate Bridge, you drop a heavy rock. How many seconds does it take to hit the water, 77 meters below? How fast is it moving when it hits the water? VIDEO EXAMPLE: From San Francisco's Golden Gate Bridge, you throw a heavy rock downwards with an initial speed of 2.0 m/sec. How far does the rock fall in 3.0 seconds? How fast is it moving after 3.0 seconds? VIDEO EXAMPLE: From San Francisco's Golden Gate Bridge, you throw a heavy rock upwards with an initial speed of 2.0 m/sec. How far does the rock fall in 3.0 seconds? How fast is it moving after 3.0 seconds? VIDEO EXAMPLE: From San Francisco's Golden Gate Bridge, you throw a heavy rock upwards with an initial speed of 2.0 m/sec. When does it hit the water, 77 meters below? How fast is it moving when it hits the water? |
Additional Activities & Practice (Ignore air resistance for these problems.)
1. How much time does it take a rock dropped from the top of the Sears Tower in Chicago (one of the world's tallest buildings, 440 m tall) to hit a pedestrian in the street?
2. How much time does it take a parachutist (whose parachute has failed to open) to hit the ground, if the parachutist jumped from a hot air balloon hovering at a height of 3000 m?
3. How much time does it take for a rock, dropped from your height, to hit the ground?
4. After jumping out of a hovering helicopter, how far will a parachutist fall in one minute, before opening the parachute?
5. Determine your average reaction time. For this activity you need a helper, like a parent or sibling, and a meterstick. Have your helper hold the meterstick from the 100-cm end, dangling vertically. You put your thumb and forefinger to either side of the stick, at the 0-cm mark. The helper should drop the stick without warning, and you grab the stick without moving your hand vertically. Record the distance the stick fell. Repeat a total of five times and take the average. (If you use a yardstick, convert your average measurement into meters.) Now calculate your average reaction time. (If you don't have a meterstick or yardstick at home, you can use any long object and then measure with your regular ruler, or borrow one of my metersticks during a free period or break.)
6. You are driving a car at 65 miles per hour when a cute, adorable puppy
runs out onto the highway right in front of you. You can't even react (hit
the brakes) for at least the time you found in problem 5, your reaction
time. How far will your car move before you can even hit the brakes?
7. Calculate how far a dropped object will fall in (a) 0.10 sec, (b) 0.20 sec, (c) 0.30 sec, (d) 0.40 sec, (e) 0.50 sec
8. The Dodge Viper SRT10 roadster sells for about $86,000.
(a) One reason the Viper is so expensive is that it can accelerate
from rest to 60 miles per hour in 3.8 seconds. Calculate the acceleration
of the car in m/sec². (Hint: Convert 60 mi/hr into m/sec first.)
(b) It's deceleration
performance is impressive, too,
being able to brake from 60 miles per hour to a stop in a distance of 100
feet. Calculate the acceleration in m/sec². (Hint: convert 100
feet into meters first.)
9. If you throw a ball straight upwards at a speed of 40 m/sec, how fast is it moving after 1 sec, after 2 sec, after 3 sec, etc, until 10 seconds. (Use g=-10 m/sec².)
10. Convert the acceleration of gravity, 9.8 m/sec², into miles per hour per second.
11. A ball is thrown straight upwards at an initial speed of 35 m/sec. (a) How many seconds will it take to come to a stop? (b) What is its velocity 3.0 seconds after it is thrown? (c) What is its velocity 5.0 seconds after it is thrown? (Use g=-10 m/sec².)
12. Calculate the position of the ball in Problem 11, at (a) the time it is at a stop, at the peak of its flight, (b) 3.0 seconds after being thrown, and (c) 5.0 seconds after it is thrown. Use y for the position, instead of x, because this is a vertical motion problem. Take y=0 to be point at which the ball is released from the hand.
13. A ball is thrown upwards at an angle, but the vertical component of the initial velocity is 35 m/sec (same as the previous two problems). The horizontal component of the initial velocity is 10 m/sec and doesn't change, because gravity doesn't pull sideways. What is the x-position and the y-position of the ball (a) at the peak of its path, (b) at 3.0 seconds after it is thrown, and (c) 5.0 seconds after it is thrown?
14. A spaceship is coasting at 12 km/sec when the pilot fires the engine, causing the ship to speed up at a rate of 0.10 km/sec². (a) After 1.0 minutes, how fast is the ship moving? (b) What distance did the ship travel during that minute? (c) Sketch graphs of x(t) and v(t) for the ship.
15. Create a spreadsheet that, given an initial velocity and an acceleration of an object, calculates its position every half-second from 0 seconds to 10 seconds. The initial velocity and acceleration should be single cells, but the time will be a column: 0, 1, 2, ..., up to 10. The distance column will be a formula, the equation ![]() , with the initial velocity and acceleration referencing their respective cells using absolute references or cell names.
, with the initial velocity and acceleration referencing their respective cells using absolute references or cell names.
16. Here is the velocity graph of a car that is traveling in a straight line. (a) What is the total distance traveled during these twenty seconds? (b) What is the acceleration between t=12 sec and t=20 sec? (c) Sketch the corresponding distance-versus-time graph, labeling the axes completely.
|
|
17. At the surface of Europa, a moon of Jupiter, g = 1.314 m/sec2. If you were standing on Europa, and threw a ball straight upwards at the speed of a good baseball pitch (90 miles per hour), how much time would it take to reach its “apogee”? How high would the ball go? (a) First, convert the speed to m/sec. (1 mi = 1609 m). Use the FL method. (b) Now, calculate the time needed to reach the “apogee”. (c) Lastly, calculate the height of the “apogee”. |
18. The Lincoln Financial Building in downtown Greensboro is 114 meters high. You drop a bowling off off the top of the building.
(a) How much time does it take the ball to hit the ground?
(b) How much time does it take to fall only halfway to the ground?
(c) What percentage is the time to fall halfway, of the total time needed to reach the ground?
19. Mars has two moons, both of which are small and thought to be asteroids captured by Mars’s gravity. Deimos is the smaller of the two, only 15 km long in its longest axis. (It’s not quite round.) The acceleration due to gravity at its surface is only 0.0039 m/sec2. You are an astronaut who has just landed on Deimos.
|
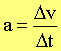
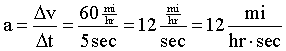

graph1.png)

graph2.png)