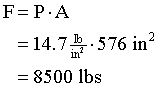Pressure
Introduction Pressure is defined as a force per unit area. In an equation, that's
That's the mathematical definition, but what does it mean? Here are some examples from everyday life:
- Have you ever dived to the bottom of a swimming pool? It feels like your head is getting squished. Well, it is! The deeper you go in the water, the greater the pressure. The pressure is greater lower in the water, because the water deep down is holding up the water overhead.
- Have you ever pumped up a bike tire or car tire? You have to put in enough air to reach the right pressure, which the usually stamped on the side of the tire. My bike tires are supposed to be pressurized to 120 pounds (of force) per square inch (of area). It's written 120 PSI on the tires. The air molecules inside each tire's inner tube are pressing outwards with 120 pounds against each square inch of rubber. If you put in too much air, the tube will pop; with too little air, the tire will be "flat".
- Have you ever tried walking on top of snow? Sometimes you can do it, especially if there's a glaze of ice on top, you walk slowly, and shuffle your feet. Why does shuffling your feet help? If you keep both feet always on the snow, your weight is being supported by a greater area – more snow. Greater area (look at the equation) means less pressure. Snowshoes work because they distribute your weight over an area far larger than the area of your feet, so a lot of snow can share the job of holding up your weight.
- Have you ever accidentally tried cutting something (chicken at dinner, maybe) with the wrong edge of the knife? Knives work because the sharp edge has a small area, so when you press that small area, A, against the chicken with force F, you create a large pressure. Another way to think of it is that with a small area of contact, there aren't as many chicken atoms pushing back against the knife as there would be if you used the knife's dull side.
What causes pressure? It's just atoms and molecules bashing into each other. Water molecules at the bottom of the swimming pool bouncing off the molecules of your head, air molecules bouncing off the rubber of a tire's inner tube, shoe molecules bouncing off the water molecules of snow, iron atoms of a knife bouncing off chicken molecules. It is the normal force — our old frind FN — divided by area. The pressure of a fluid operates normal (perpendicular) to the surface, regardless of the surface's orientation. This is called Pascal's Principle, after its discoverer Blaise Pascal (French, 1623-1662).
The atoms bang against each other because either
- there are lots of them in a small volume (like air molecules inside a bike tire), or
- they are being squeezed together by an outside force, like gravity (as in the swimming pool or walking on snow) or a person (as in cutting food with a knife).
Activities & Practice
to do as you read
1. Women wearing high heels have a difficult time walking across lawns. Why?
2. Here's a video mystery: can you explain why the balloon is so hard to pop?
Atmospheric Pressure At the bottom of a swimming pool, the pressure is equal to the weight of the overlying water divided by the area that weight is pressing against. The same idea applies in the atmosphere. For every square meter of the surface of the Earth, the full weight of all the air above that square meter, extending all the way up to space, is pressing down. This is called atmospheric pressure. Atmospheric pressure is less when you go up a mountain, because the higher you go the less air is above you. This is why air is denser at lower altitudes; the greater pressure squeezes more air molecules into each cubic centimeter.
In class we recreate the 1650 Magdeburg experiment, in which Otto von Guericke demonstrated the existence of air pressure and his invention of the air pump. Two hemispheres are joined together and the air between them removed, creating a vacuum inside. Atmospheric pressure on the outside presses the two hemispheres tightly together, making them very difficult to separate. Read more about the Magdeburg experiment in the Wikipedia article "Magdeburg Hemispheres."
When you go flying, or drive up a mountain road, it feels like your head is going to pop. There is some air inside your head, in the sinuses and inner ear. On the ground, the air pressure inside those cavities is equal to the atmospheric pressure outside your head. The net force is zero and you feel fine. But when you suddenly gain altitude, the outside air pressure decreases rapidly. The pressure inside your head is greater than outside, creating a net force outwards that can be painful. Eustachian tubes connect your mouth (and the atmosphere) to the inside of your head, allowing air molecules to flow from high pressure to low pressure, equalizing the pressure. That's why you feel OK after a while. You can speed up that process by chewing gum: the movement of the jaws flexes the Eustachian tubes, helping the air bubbles work their way through.
Far outside the Earth's atmosphere, space itself is essentially a vacuum, with almost no pressure because there are almost no gas atoms.
Units Pressure is measured in a variety of units. In SI, the standard unit is the N/m², which is also called the Pascal (abbreviated Pa) in honor of Blaise Pascal. A bar is equal to 100,000 Pa; a millibar is more commonly used, and is equal to 100 Pa. The usual English unit for pressure is the pound/inch², commonly abbreviated psi.
Atmospheric pressure is measured with barometers, of which there are two types: liquid-column and anaeroid.
Pressure can be indicated by the height of a mercury (Hg) column in a liquid-column barometer (see diagram, below left), in either millimeters or inches.
Liquid-column barometers are not terribly common, because they are large and inconvenient, not to mention that the mercury is toxic. Instead, you are more likely to own or see an aneroid barometer (see photo, above right). Here's a diagram showing how an aneroid barometer works.
The average atmospheric pressure at sea level is
101.3 kPa = 1013 mbar = 14.7 psi = 29.92 inHg = 760 mmHg = 1 atm
This is the average. The movement of weather systems causes atmospheric pressure to fluctuate. As a general rule, increasing pressures indicate clear skies and calm weather; decreasing pressures foretell clouds, rain or storms.
The decrease of air pressure with increasing altitude is used in aircraft altimeters. They are essentially aneroid barometers, only instead of reading one of the standard pressure units above, display altitude.
2. A standard-size brick is 2.25" x 3.5" x 8" and weighs 3.5 pounds. (a) What is the pressure exerted, in psi, by a brick laying flat on a table? (b) What is the pressure it exerts if standing up on one end? (c) Convert both previous answers into Pascals.
Example A standard "two-by-four" is actually 1.5" x 3.5". An eight-foot length of this wood weighs about 9 pounds. (a) How much pressure, in psi, is it exerting on the ground, if stood on end? (b) Convert your answer to Pascals.
(a) The area of the end of the board is 1.5 inch x 3.5 inch = 5.25 inch².
P = F/A = 9 lbs / 5.25 inch² = 1.7 lbs/inch².
(b) Use the factor-label method, and don't forget to square the inches-to-meters conversion factor.
Example How much force does the atmosphere exert on the outside surface of a square window, 2.0 feet on a side.
Since P = F/A, then F = P·A. We'll use barbaric units, since that's what we were given. Atmospheric pressure is 14.7 lb/in2, so we need to know the area in square inches. The side of the window is 24 inches, so the area is (24 inches)2 = 576 in2.
Here's a solution video for this example.
Fluid Pressure For a fluid of constant density ρ on a planet with gravitational field strength g, the pressure at a depth h is equal to
Proof: Pressure is the weight of fluid pressing down on every unit of area at depth h. Consider a horizontal area A, and we'll calculate the weight of the fluid in the column above that area.
If you'd prefer to see a narrated video of this proof, click the thumbnail below:
4. How deep do you have to go in a swimming pool in order for there to be one atmosphere's worth of pressure due to the water?
Additional Activities & Practice
5. Estimate the pressure a ball-point pen exerts on paper when someone
is writing.
6. How deep would you have to dive into a pool of mercury, in order for the added pressure to equal one atmosphere?
7. The deepest point of Earth's oceans, the bottom of the Mariana Trench, is 10,923m deep! The US Navy research submersible Trieste was the first vessel to reach this point, in 1960. What pressure did the Trieste have to withstand? Give your answer in psi, Pa, and atmospheres. (NOTE: the density of seawater is about 1025 kg/m³.)
8. Which one of these locations has the greatest pressure? (A) ten meters below the surface of Lake Brandt, (B) ten meters below the surface of Lake Michigan, (C) ten meters below the surface of a deep swimming pool?
9. A cube, one meter on a side, is located with its top 20 meters below the surface of a fresh-water lake. (a) What is the pressure at the top of the cube? (b) What is the force pressing down on the top of the cube? (c) What is the pressure at the bottom of the cube? (d) What is the force pressing up on the bottom of the cube? (e) What is the net force of forces (b) and (d)?
10. This suction-cup ball is stuck on a window. Can you explain how suction cups work?
11. The density of air near the surface of Earth, on a typical day at 20°C, is about 1.2 kg/m3. How much height do you need to rise, in order for the air pressure to decrease by 1.0 Pa?
12. Write a paragraph explaining in detail why this happens? Here's a larger event, same idea.