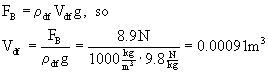Buoyancy Problem Solutions

Problem Solutions

1. A standard basketball (mass = 624 grams; 24.3 cm in diameter) is held fully under water. Calculate the buoyant force and weight. When released, does the ball sink to the bottom or float to the surface? If it floats, what percentage of it is sticking out of the water? If it sinks, what is the normal force, F_N with which it sits on the bottom of the pool? SOLUTION The weight of the ball is To calculate the buoyancy, we need the volume of displaced water, which is the volume of the ball because it is being held completely submerged. The buoyant force is equal to the weight of that volume of water. That's a lot stronger than the 6.1N downward pull of gravity, so the ball will rise to the surface when released. The density of the ball is which is 8.3% the density of water. The ball will therefore be floating with 8.3% of its volume below the level of the surface, and 91.7% sticking out of the water.
2. Six objects (A-F) are in a liquid, as shown. None of them are moving. Arrange them in order of density, from lowest to highest. SOLUTION: The more of an object's volume is above the water surface, the less dense it is. Object B must therefore be the least dense, followed by D, A, and F. Object E is next, because it is neutrally buoyant and equal in density to the liquid. Object C is negatively buoyant because it is more dense than the fluid. Full answer to the question: B, D, A, F, E, C.
3. Water ice has a density of 0.91 g/cm³, so it will float in liquid water. Imagine you have a cube of ice, 10 cm on a side. (a) What is the cube's weight? (b) What volume of liquid water must be displaced in order to support the floating cube? (c) How much of the cube is under the surface of the water? SOLUTION: (a) The cube's weight is (b) The buoyant force must equal the cube's weight. Take the equation for buoyant force, solve it for V_df, and plug in the numbers. (c) The volume of the cube itself is 0.001m³, so the percentage under the surface is... This detailed calculation confirms our rule-of-thumb that the ratio of an object submerged is the same as the ratio of its density to that of the fluid in which it is immersed. This also confirms the old adage that when you see an iceberg floating in the ocean, it really is "just the tip of the iceberg." 4. You have a block of a mystery material, 12 cm long, 11 cm wide and 3.5 cm thick. Its mass is 1155 grams. (a) What is its density? 2.5 g/cm³ or 2500 kg/m³ (b) Will it float in a tank of water, or sink? It's more dense than the water, so it's gonna sink! (c) If it floats, what percentage of the object will be sticking out above the water? If it sinks, what will be the normal force it presses against the bottom of the tank? When the block sits on the bottom of the tank, there are 3 forces acting on it: gravity (a.k.a. weight, downwards), buoyancy (upwards) and the normal force (upwards). The block is in equilibrium (F_NET=0) so the magnitude of upwards forces must equal the downwards force of gravity. In other words, F_g= F_B+ F_N The weight, F_g= m g = 1.155 kg * 9.8 N/kg = 11.3 N The buoyant force, F_B= density of fluid * volume * g = 4.5 N Therefore, the normal force F_N= 6.8 N (d) Repeat parts b and c, only instead of water, the tank is full of mercury. The object is less dense than mercury (13.6 g/cm³), so the object will float in mercury. The ratio of their densities, is 2.5/13.6 = 0.18. So 18% of the object is below the surface of the mercury, meaning that 82% must be sticking up above the surface.