Electric Fields
As you already know, electric charges exert forces on each other. Imagine that you have a set of charges --- some big, some small, some positive, some negative --- scattered around. Now imagine that you have a small test charge that you can move around, and at many places you stop and measure the force exerted on the test charge by all the other charges. The force felt by that test charge is the vector sum (i.e. the resultant) of the forces exerted on it by each individual charge. This is called the principle of superposition.
Here are some diagrams to illustrate this concept. Red circles represent positive charges; black circles are negative. The test charge is positive, and drawn smaller than the others.
In this first diagram, both charges are negative, and so both attract the test charge. Because they are in opposite directions, however, the resultant (net) force is zero.
If we now make both the big charges positive, the forces become repulsive. They are still in opposite directions, however, so the net force is still zero.
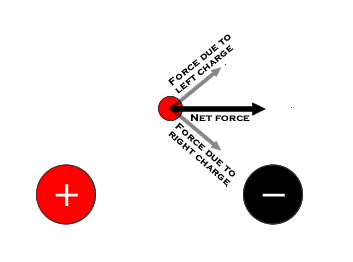
Below, the test charge is repelled from the positive charge and attracted to the negative charge. Both of these forces point to the right, so the net force is to the right.
Here, the test charge is no longer directly between the two big charges, so the two forces are no longer parallel.
Now, imagine we move the test charge to many, many points. At each point you stop and draw a vector showing the force felt by the test charge at that point. (You don't draw the test charge anymore, because the test charge was moved everywhere around the other charges.) What you get, for a positive charge next to a negative charge, is shown here:
The resulting picture is called the electric field: at any point, the electric field points in the direction a positive charge would be pushed. The picture above was created using the PhET Charges and Fields applet. The arrows show the direction of the net force at each point; the darker the arrow, the stronger the force.
Activities & Practice
to do as you read
1. Play with the Charges and Fields applet, making some electric fields. Click the "Show E-field" checkbox, then drag over some positive and/or negative charges from the storage boxes on the upper right. Now, answer the following questions.
a. If you have a single, isolated positive charge, in what direction do the electric field lines point? Make a sketch.
b. In what direction do the electric field lines point around a single, isolated negative charge? Make a sketch.
c. If you have a mixture of positive and negative charges, the electric field always flows outward from ____ charges and towards ____ charges.
2. Play Electric Field Hockey: the hockey puck is a positive charge, and you use other charges to create an electric field that pushes the puck around obstacles and into the goal. This will be for a grade --- follow all these directions and do not share your solution with others. Turn on the "field" and "trace" options. Get a goal on Difficulty level 2 and you'll get a 90% grade. Get a goal on Difficulty level 3 for 100%. The person who gets a goal on Level 3 with the lowest number of charges will get 110%. You are not allowed to move the charges while the puck is moving: set it up and let it run its course. Then tweak the positions of the charges. Also, the puck must stay on the screen, and you are allowed a maximum of 25 charges.
When you have gotten your goal, hit the Print Screen (PrtSc) button on your keyboard (on my laptop, it's above F11) or use the Screen Sni Tool. This will create a screenshot. Then open an email to me and paste the image directly into the message (with Ctrl-V) and send it. Do NOT send the picture as an attachment.
Electric Field Lines Computers are good at doing many repetitive calculations very fast, like the calculations the PhET Charges and Fields applet does to make the above diagrams. For humans, however, drawing vectors at many places around some charges can be tedious, to say the least. There's a shortcut way to draw an electric field. We draw electric field lines instead of lots of separate vectors. Electric field lines are tangent to the vectors everywhere. Here's an example — the same two charges as the picture above, only with the field lines added in green.
You don't need the vectors there in order to draw a rough sketch of the electric field lines. Here are a few simple rules to follow:
- field lines flow out of positive charges, and inward toward negative charges
- field lines cannot cross
- field lines curve away from positive charges and towards negative charges
The electric field is strongest where the field lines are closest.
3. Draw the electric field around two equal positive charges. SOLUTION VIDEO
4. Draw the electric field around four charges, two positive and two negative, arranged in a square with like charges in opposite corners. SOLUTION VIDEO
Additional Activities & Practice
5. Imagine there are two charges, 3.0 ncoul and -5.0 ncoul, located at (0,0) and (1,2) meters, respectively.
(a) Calculate the magnitude, x-component, and y-component of the electric field at the point (1,1) meters, due to the charge at (0,0).
(b) Calculate the magnitude, x-component, and y-component of the electric field at the point (1,1) meters, due to the charge at (1,2).
(c) Calculate the total x-component, total y-component, and resultant magnitude of the electric field at (1,1).
6. SPREADSHEET: Create a spreadsheet that calculates the total electric field at any point (in 2-dimensions) due to two charges located anywhere. There should be eight input cells: the two charges (in coulombs), their x- and y-coordinates, and the coordinates of the point P where you want to know the electric field. The output should be four cells: the x- and y-components of the total electric field at P, and its magnitude and (mathematical) direction.