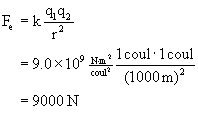Coulomb's Law
In 1784 Charles-Augustin de Coulomb, a French physicist and military engineer, discovered that the force between two charged objects was, like gravity, inversely proportional to the square of the distance between them. He did this by using a torsion balance. Here's a photo of it. A horizontal bar is suspended from its middle by a thin wire. At the ends of that bar are two small spheres, and the whole bar is free to rotate around the wire suspending it. Not attached to the bar are two other spheres near to, but not touching, the spheres on the bar. These other spheres are so placed that, when charged and attracting (or repeling) the bar spheres, they exert a torque (twisting force) on the bar. By measuring the charge and the twist of the wire, the dependence of the electric force on the amount of charge can be studied, as well as the effect of distance.
What Coulomb found was that the force acting between two charges is proportional to both of the charges, and inversely proportional to the square of the disance between them. Boiling that long sentence into an equation gives us Coulomb's Law:
Fe is the force of attraction or repulsion between the two charges, q1 and q2, when they are separated by a distance r.
Does this look familiar? It's very similar to Newton's gravitation equation,
Both equations are inverse-square relationships: doubling the distance causes the force to drops by a ratio of 4, for example. The force is proportional to some property of the two objects — charge in the case of the electric force, mass in the case of gravity. In each equation there is a constant of proportionality that describes the strength of the force, and which causes the result to have the unit of force. You will recall that
For the electric force, the constant of proportionality is
Notice that k is extremely large compared to G. Although the size of these numbers is determined in part by the sizes of the coulomb and kilogram, nonetheless the electric force is a much stronger phenomenon than gravity. Although the equations for electric and gravitational forces look the same, there is one very important but hidden difference between them — charge comes in opposite polarities, positive and negative. The net charge on most objects is zero, making the electric force zero. Conversely, mass is always positive, so one mass can’t cancel the effects of another mass. That’s why gravity dominates the Universe, even though G is so small.
Activities & Practice
to do as you read
1. Calculate the electric force between a proton and electron in a Hydrogen atom, where they are separated by an average distance of 0.0529 nm. (The charge on each is ±e, but express that in coulombs in the calculation.)
2. Calculate the gravitational force between the proton and electron in the Hydrogen atom. (Their masses are 1.67x10-27kg and 9.11x10-31kg, respectively, and the distance is the same as in problem 1.)
EXAMPLE What is the electric force between two 1-coulomb charges, separated by 1 km?
Additional Activities & Practice