Introduction to Trigonometry
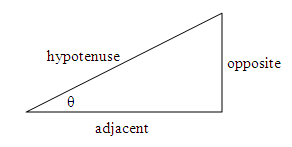
We did an activity where you measured the sides of similar triangles. (Triangles are said to be "similar" if they have the same shape, and differ from each other only in size.) With a right triangle with a particular angle, θ, you found that the ratio of the opposite side divided by the hypotenuse is the same, regardless of the size of the triangle. This is an interesting, and as it turns out, very useful mathematical pattern! In the example we did, the angle θ was 27°, and the ratio opposite/hypotenuse was 0.45. That is, the side opposite the 27° corner is always 45% the length of the hypotenuse. This is true of all right triangles with a 27° corner, be they small, medium or large, or microscopic or gargantuan.
Because of this interesting pattern, the ratio opposite/hypotenuse for a right triangle has been given a special name. It is called the sine function, abbreviated sin(θ). Other ratios of the sides of a right triangle follow the same pattern. These are the cosine function (=adjacent/hypotenuse) and the tangent function (=opposite/adjacent)
To summarize: For a right triangle, with one of the corners having angle θ, the following functions sine, cosine and tangent are defined as follows:
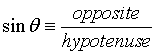
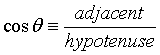
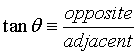
"Opposite" is the length of the side of the triangle opposite angle θ, "hypotenuse" is the length of the longest side, and "adjacent" is the length of the other side, next to the angle θ.
Here's a simple mnemonic device to help you remember these definitions: SOHCAHTOA.
SOH — sine is opposite over hypotenuse
CAH — cosine is adjacent over hypotenuse
TOA — tangent is opposite over adjacent
What makes these functions so useful is that your calculator will tell you the value of any of these ratios, for any angle θ. (In the old days before computers and calculators, people looked up the values in long tables, usually in an appendix at the back of the math or physics book.) So, if you know the length of one side of a right triangle, and the angle of one corner (other than the 90° corner), you can easily determine the length of the other two sides.
Activities & Practice
to do as you read
1. Use your calculator to determine the value of sin(27°). On some calculators you enter "27" first, then hit the "sin" key. On others you hit "sin" first, then enter the number. Play with your calculator to learn which way it works. Also, there are units used to measure angles other than degrees. The most common of these are the radian and the grad. We won't be using them, but you have to make sure your calculator is in "degree mode". On the TI graphing calculators, hit the MODE key and scroll down a few lines. Make sure DEGREES is highlighted, not RADIANS. On many other calculators, there is a key marked DRG (for degrees, radians, grads). Hit that until a small D appears on the display.
When the mode it set right, you should get 0.45 as your result of sin(27°).
Here are two examples:
- You are standing a distance of 55 meters from the base of a flagpole. By sighting along a protractor that has a string and hanging weight, you determine that the top of the pole is 35 degrees above the horizontal from your vantage point. How high is the flagpole? WATCH VIDEO
- A circus performer is shot out of a cannon with a speed of 25 m/sec at an angle 40.0° above the horizontal. What is the performer's (a) horizontal and (b) vertical speed when emerging from the cannon? WATCH VIDEO
Additional Activities & Practice
2. A basketball player launches the ball at a velocity of 6.0 m/sec, 45° above the horizontal. What are the (a) horizontal and (b) vertical components of the velocity?
3. Leaving the entrance of the cafeteria, you walk 55 meters in the direction 25° North of East. (a) How far east did you go? (b) How far to the north did you go?
4. The Leaning Tower of Pisa is currently leaning at an angle of 3.99 degrees from vertical, and is 45 meters high, along the slant, to the top level where you can stand. If you drop a ball from the top, right at the edge, how far from the base will it land?
5. The radius of Earth is about 6400 km. At the latitude of Greensboro (36° N), how far are we from the Earth's axis?
6. The image below is from the HiRISE camera on the Mars Reconnaissance Orbiter probe, in orbit around Mars, and was taken on 26 June 2007. (Click on it to see a larger version.) The fuzzy thing is a dust devil — we're looking down on it — and you can see the dust devil's shadow. At the time the picture was taken, the Sun was 48° above the horizon. Overall, the picture is 4.0 km wide. How tall is the dust devil?