ISOLATING A VARIABLE

Here's a video version of the following text, narrated by a chipmunk.

Introduction In math class, x is usually used for the unknown. Physicists and astronomers usually use other letters to stand for the quantities they are interested in. For example, ‘F’ represents a force, ‘a’ is acceleration, ‘d’ stands for distance, 'm' is mass, and so on. If we used 'x' for everything, it would get very confusing! Don’t let the fact that we’re not using x like you do in math class confuse you. What letter is used doesn’t matter!

The word “equation” means that you have two things equal to each other. To signify that, we put an equals sign ‘=‘ between them. This may sound like I'm talking down to you, but I do want to stress that an equals sign is a very strong statement. The two sides of the equation are the same, they are interchangable.

The phrase “Solve the equation” means to rearrange the parts of the equation to isolate (get by itself) what you are interested in knowing. For instance, if we have the equation

and we want to calculate "a" (the acceleration), we need to get "a" by itself, on either the left or right side of the equation. The easiest way to do this is to get rid of the "m" (the mass). But we can't just erase the "m" — if we did that, the equals sign would no longer be true! So what do we do?

Here's the way you should reason it out: What is the "m" doing to the "a"? It's multiplying it. So to get rid of that multiplication, we need to undo the multiplication; we need to do the opposite. What's the opposite of multiplying? Right! Dividing! So divide both sides of the equation by the mass, m. We do it to both sides in order to keep the equals sign true: if two things start out the same, and then you divide both by the same number, they remain equal to each other. Doing this, we get...

which then becomes

(Because m/m is 1, they "cancel out"). We're done! Now that we have the acceleration by itself, if we know the force ("F") and the mass ("m") we can plug in those numbers to calculate "a".

The method described above is completely general: whatever operations (things like multiplication, division, addition, etc...) are happening TO the thing you are trying to isolate, you need to UNDO them by doing the opposite (inverse) operation.

• Addition & subtraction are inverse operations.
• Multiplication & division are inverse operations.
• Raising to power n and power 1/n are inverse operations. For instance, squaring (raising to 2nd power) and square roots (raising to power ½). Likewise for cubing and cube roots.

Activities & Practice
to do as you read.

1.

Solve this for v.

Solve this for t.

2.

Solve this for f.

Solve this for λ.

3.

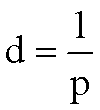
Solve for p.

4.

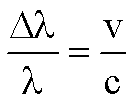
Solve for v.

Solve for Δλ.

Solve for λ.

Another example Let's look at a harder example. Let's say you want to isolate the "t" (time) in this equation:

What is being done TO the "t"? It's being squared first, and then multiplied by "a/2". That's the order, because whenever you see a mathematical expression, the operations occur in PEMDAS order. What's that, you ask? Operations in parentheses always have the highest priority: they're done first (but there weren't any parentheses in our example.) Then comes exponentiation (the squaring done to the t in this example), then multiplication & division, and lastly addition & subtraction. The first letters spell out "pemdas", which is an easy way to remember the order.

So, now that we know what's being done to the "t", we have to undo it all, by doing the inverse operations in reverse order. Here goes...

First, divide by a/2:

(Remember, do everything to both sides!)

Then simplify:

(The "cancel" on the right-hand side, and on the left side, dividing by half is the same as multiplying by two.)

Undo the squaring by taking the square root:

At last, we arrive at the end . TA DA!

5.

Solve for m.

Solve for c.

6.

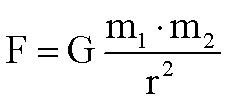
Solve for G.

Solve for d.

Solve for m₁.

7.

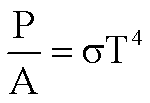
Solve for P.

Solve for A.

Solve for σ.

Solve for T.

Additional Activities & Practice

8.

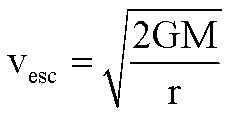
Solve for M.
Solve for G.
Solve for R.

9.

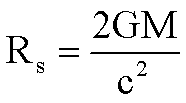
Solve for M.
Solve for G.
Solve for c.

10.

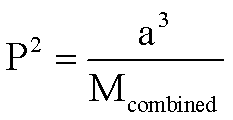
Solve for P.
Solve for a.
Solve for M_combined.

11.

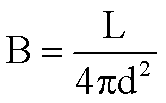
Solve for L.
Solve for d.